| The FACTOR Procedure |
Example 33.3 Maximum Likelihood Factor Analysis
This example uses maximum likelihood factor analyses for one, two, and three factors. It is already apparent from the principal factor analysis that the best number of common factors is almost certainly two. The one- and three-factor ML solutions reinforce this conclusion and illustrate some of the numerical problems that can occur. The following statements produce Output 33.3.1 through Output 33.3.3:
title3 'Maximum Likelihood Factor Analysis with One Factor'; proc factor data=SocioEconomics method=ml heywood n=1; run;
title3 'Maximum Likelihood Factor Analysis with Two Factors'; proc factor data=SocioEconomics method=ml heywood n=2; run;
title3 'Maximum Likelihood Factor Analysis with Three Factors'; proc factor data=SocioEconomics method=ml heywood n=3; run;
Output 33.3.1 displays the results of the analysis with one factor.
| Maximum Likelihood Factor Analysis with One Factor |
| Input Data Type | Raw Data |
|---|---|
| Number of Records Read | 12 |
| Number of Records Used | 12 |
| N for Significance Tests | 12 |
| Maximum Likelihood Factor Analysis with One Factor |
| Prior Communality Estimates: SMC | ||||
|---|---|---|---|---|
| Population | School | Employment | Services | HouseValue |
| 0.96859160 | 0.82228514 | 0.96918082 | 0.78572440 | 0.84701921 |
| Preliminary Eigenvalues: Total = 76.1165859 Average = 15.2233172 |
||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | 63.7010086 | 50.6462895 | 0.8369 | 0.8369 |
| 2 | 13.0547191 | 12.7270798 | 0.1715 | 1.0084 |
| 3 | 0.3276393 | 0.6749199 | 0.0043 | 1.0127 |
| 4 | -0.3472805 | 0.2722202 | -0.0046 | 1.0081 |
| 5 | -0.6195007 | -0.0081 | 1.0000 | |
| Iteration | Criterion | Ridge | Change | Communalities | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 6.5429218 | 0.0000 | 0.1033 | 0.93828 | 0.72227 | 1.00000 | 0.71940 | 0.74371 |
| 2 | 3.1232699 | 0.0000 | 0.7288 | 0.94566 | 0.02380 | 1.00000 | 0.26493 | 0.01487 |
| Significance Tests Based on 12 Observations | |||
|---|---|---|---|
| Test | DF | Chi-Square | Pr > ChiSq |
| H0: No common factors | 10 | 54.2517 | <.0001 |
| HA: At least one common factor | |||
| H0: 1 Factor is sufficient | 5 | 24.4656 | 0.0002 |
| HA: More factors are needed | |||
| Chi-Square without Bartlett's Correction | 34.355969 |
|---|---|
| Akaike's Information Criterion | 24.355969 |
| Schwarz's Bayesian Criterion | 21.931436 |
| Tucker and Lewis's Reliability Coefficient | 0.120231 |
| Eigenvalues of the Weighted Reduced Correlation Matrix: Total = 0 Average = 0 |
||
|---|---|---|
| Eigenvalue | Difference | |
| 1 | Infty | Infty |
| 2 | 1.92716032 | 2.15547340 |
| 3 | -.22831308 | 0.56464322 |
| 4 | -.79295630 | 0.11293464 |
| 5 | -.90589094 | |
The solution on the second iteration is so close to the optimum that PROC FACTOR cannot find a better solution; hence you receive this message:
Convergence criterion satisfied.
When this message appears, you should try rerunning PROC FACTOR with different prior communality estimates to make sure that the solution is correct. In this case, other prior estimates lead to the same solution or possibly to worse local optima, as indicated by the information criteria or the chi-square values.
The variable Employment has a communality of 1.0 and, therefore, an infinite weight that is displayed next to the final communality estimate as a missing/infinite value. The first eigenvalue is also infinite. Infinite values are ignored in computing the total of the eigenvalues and the total final communality.
Output 33.3.2 displays the results of the analysis with two factors. The analysis converges without incident. This time, however, the Population variable is a Heywood case.
| Input Data Type | Raw Data |
|---|---|
| Number of Records Read | 12 |
| Number of Records Used | 12 |
| N for Significance Tests | 12 |
| Prior Communality Estimates: SMC | ||||
|---|---|---|---|---|
| Population | School | Employment | Services | HouseValue |
| 0.96859160 | 0.82228514 | 0.96918082 | 0.78572440 | 0.84701921 |
| Preliminary Eigenvalues: Total = 76.1165859 Average = 15.2233172 |
||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | 63.7010086 | 50.6462895 | 0.8369 | 0.8369 |
| 2 | 13.0547191 | 12.7270798 | 0.1715 | 1.0084 |
| 3 | 0.3276393 | 0.6749199 | 0.0043 | 1.0127 |
| 4 | -0.3472805 | 0.2722202 | -0.0046 | 1.0081 |
| 5 | -0.6195007 | -0.0081 | 1.0000 | |
| Iteration | Criterion | Ridge | Change | Communalities | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.3431221 | 0.0000 | 0.0471 | 1.00000 | 0.80672 | 0.95058 | 0.79348 | 0.89412 |
| 2 | 0.3072178 | 0.0000 | 0.0307 | 1.00000 | 0.80821 | 0.96023 | 0.81048 | 0.92480 |
| 3 | 0.3067860 | 0.0000 | 0.0063 | 1.00000 | 0.81149 | 0.95948 | 0.81677 | 0.92023 |
| 4 | 0.3067373 | 0.0000 | 0.0022 | 1.00000 | 0.80985 | 0.95963 | 0.81498 | 0.92241 |
| 5 | 0.3067321 | 0.0000 | 0.0007 | 1.00000 | 0.81019 | 0.95955 | 0.81569 | 0.92187 |
| Significance Tests Based on 12 Observations | |||
|---|---|---|---|
| Test | DF | Chi-Square | Pr > ChiSq |
| H0: No common factors | 10 | 54.2517 | <.0001 |
| HA: At least one common factor | |||
| H0: 2 Factors are sufficient | 1 | 2.1982 | 0.1382 |
| HA: More factors are needed | |||
| Chi-Square without Bartlett's Correction | 3.3740530 |
|---|---|
| Akaike's Information Criterion | 1.3740530 |
| Schwarz's Bayesian Criterion | 0.8891463 |
| Tucker and Lewis's Reliability Coefficient | 0.7292200 |
| Eigenvalues of the Weighted Reduced Correlation Matrix: Total = 19.7853157 Average = 4.94632893 | ||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | Infty | Infty | ||
| 2 | 19.7853143 | 19.2421292 | 1.0000 | 1.0000 |
| 3 | 0.5431851 | 0.5829564 | 0.0275 | 1.0275 |
| 4 | -0.0397713 | 0.4636411 | -0.0020 | 1.0254 |
| 5 | -0.5034124 | -0.0254 | 1.0000 | |
| Factor Pattern | ||
|---|---|---|
| Factor1 | Factor2 | |
| Population | 1.00000 | 0.00000 |
| School | 0.00975 | 0.90003 |
| Employment | 0.97245 | 0.11797 |
| Services | 0.43887 | 0.78930 |
| HouseValue | 0.02241 | 0.95989 |
The results of the three-factor analysis are shown in Output 33.3.3.
| Input Data Type | Raw Data |
|---|---|
| Number of Records Read | 12 |
| Number of Records Used | 12 |
| N for Significance Tests | 12 |
| Prior Communality Estimates: SMC | ||||
|---|---|---|---|---|
| Population | School | Employment | Services | HouseValue |
| 0.96859160 | 0.82228514 | 0.96918082 | 0.78572440 | 0.84701921 |
| Preliminary Eigenvalues: Total = 76.1165859 Average = 15.2233172 |
||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | 63.7010086 | 50.6462895 | 0.8369 | 0.8369 |
| 2 | 13.0547191 | 12.7270798 | 0.1715 | 1.0084 |
| 3 | 0.3276393 | 0.6749199 | 0.0043 | 1.0127 |
| 4 | -0.3472805 | 0.2722202 | -0.0046 | 1.0081 |
| 5 | -0.6195007 | -0.0081 | 1.0000 | |
| Warning: | Too many factors for a unique solution. |
| Iteration | Criterion | Ridge | Change | Communalities | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.1798029 | 0.0313 | 0.0501 | 0.96081 | 0.84184 | 1.00000 | 0.80175 | 0.89716 |
| 2 | 0.0016405 | 0.0313 | 0.0678 | 0.98081 | 0.88713 | 1.00000 | 0.79559 | 0.96500 |
| 3 | 0.0000041 | 0.0313 | 0.0094 | 0.98195 | 0.88603 | 1.00000 | 0.80498 | 0.96751 |
| 4 | 0.0000000 | 0.0313 | 0.0006 | 0.98202 | 0.88585 | 1.00000 | 0.80561 | 0.96735 |
| Significance Tests Based on 12 Observations | |||
|---|---|---|---|
| Test | DF | Chi-Square | Pr > ChiSq |
| H0: No common factors | 10 | 54.2517 | <.0001 |
| HA: At least one common factor | |||
| H0: 3 Factors are sufficient | -2 | 0.0000 | . |
| HA: More factors are needed | |||
| Chi-Square without Bartlett's Correction | 0.0000003 |
|---|---|
| Akaike's Information Criterion | 4.0000003 |
| Schwarz's Bayesian Criterion | 4.9698136 |
| Tucker and Lewis's Reliability Coefficient | 0.0000000 |
| Eigenvalues of the Weighted Reduced Correlation Matrix: Total = 41.5254193 Average = 10.3813548 | ||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | Infty | Infty | ||
| 2 | 39.3054826 | 37.0854258 | 0.9465 | 0.9465 |
| 3 | 2.2200568 | 2.2199693 | 0.0535 | 1.0000 |
| 4 | 0.0000875 | 0.0002949 | 0.0000 | 1.0000 |
| 5 | -0.0002075 | -0.0000 | 1.0000 | |
| Factor Pattern | |||
|---|---|---|---|
| Factor1 | Factor2 | Factor3 | |
| Population | 0.97245 | -0.11233 | -0.15409 |
| School | 0.15428 | 0.89108 | 0.26083 |
| Employment | 1.00000 | 0.00000 | 0.00000 |
| Services | 0.51472 | 0.72416 | -0.12766 |
| HouseValue | 0.12193 | 0.97227 | -0.08473 |
In the results, a warning message is displayed:
WARNING: Too many factors for a unique solution.
The number of parameters in the model exceeds the number of elements in the correlation matrix from which they can be estimated, so an infinite number of different perfect solutions can be obtained. The criterion approaches zero at an improper optimum, as indicated by this message:
Converged, but not to a proper optimum.
The degrees of freedom for the chi-square test are 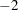 , so a probability level cannot be computed for three factors. Note also that the variable Employment is a Heywood case again.
, so a probability level cannot be computed for three factors. Note also that the variable Employment is a Heywood case again.
The probability levels for the chi-square test are 0.0001 for the hypothesis of no common factors, 0.0002 for one common factor, and 0.1382 for two common factors. Therefore, the two-factor model seems to be an adequate representation. Akaike’s information criterion and Schwarz’s Bayesian criterion attain their minimum values at two common factors, so there is little doubt that two factors are appropriate for these data.
Copyright © SAS Institute, Inc. All Rights Reserved.