| The FACTOR Procedure |
| Simplicity Functions for Rotations |
To rotate a factor pattern is to apply a nonsingular linear transformation to the unrotated factor pattern matrix. An optimal transformation is usually defined as a minimum or maximum point of a simplicity function. Different rotation methods are based on different simplicity functions employed.
For the promax or the Procrustes rotation, the simplicity function used is the sum of squared differences between the rotated factor pattern and the target matrix. The optimal transformation is obtained by minimizing this simplicity function with respect to the choices of all possible transformation.
For the class of the generalized Crawford-Ferguson family Jennrich (1973), the simplicity function being optimized is
 |
where
 |
 |
 , and
, and  are constants, and
are constants, and  represents an element of the rotated pattern matrix. Except for specialized research purposes, it is uncommon in practice to use this simplicity function directly for rotation. However, this simplicity function reduces to many well-known classes of rotations. One of these is the Crawford-Ferguson family Crawford and Ferguson (1970), which minimizes
represents an element of the rotated pattern matrix. Except for specialized research purposes, it is uncommon in practice to use this simplicity function directly for rotation. However, this simplicity function reduces to many well-known classes of rotations. One of these is the Crawford-Ferguson family Crawford and Ferguson (1970), which minimizes
 |
where  and
and  are constants,
are constants,  represents variable (row) parsimony, and
represents variable (row) parsimony, and  represents factor (column) parsimony. Therefore, the relative importance of both the variable parsimony and of the factor parsimony is adjusted using the constants
represents factor (column) parsimony. Therefore, the relative importance of both the variable parsimony and of the factor parsimony is adjusted using the constants  and
and  . The orthomax class (see Harman 1976) maximizes the function
. The orthomax class (see Harman 1976) maximizes the function
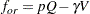 |
where  is the orthomax weight and is usually between 0 and the number of variables
is the orthomax weight and is usually between 0 and the number of variables 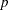 . The oblimin class minimizes the function
. The oblimin class minimizes the function
 |
where  is the oblimin weight. For practical purposes, a negative or zero value for
is the oblimin weight. For practical purposes, a negative or zero value for  is recommended.
is recommended.
All of the preceding definitions are for rotations without row normalization. For rotations with Kaiser normalization, the definition of  is replaced by
is replaced by  , where
, where  is the communality estimate of variable
is the communality estimate of variable  .
.
Copyright © SAS Institute, Inc. All Rights Reserved.