| The FACTOR Procedure |
| Confidence Intervals and the Salience of Factor Loadings |
The traditional approach to determining salient loadings (loadings that are considered large in absolute values) employs rules of thumb such as 0.3 or 0.4. However, this does not use the statistical evidence efficiently. The asymptotic normality of the distribution of factor loadings enables you to construct confidence intervals to gauge the salience of factor loadings. To guarantee the range-respecting properties of confidence intervals, a transformation procedure such as in CEFA (Browne et al.; 2008) is used. For example, because the orthogonal rotated factor loading  must be bounded between
must be bounded between  1 and
1 and 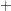 1, the Fisher transformation
1, the Fisher transformation
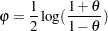 |
is employed so that  is an unbounded parameter. Assuming the asymptotic normality of
is an unbounded parameter. Assuming the asymptotic normality of 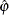 , a symmetric confidence interval for
, a symmetric confidence interval for  is constructed. Then, a back-transformation on the confidence limits yields an asymmetric confidence interval for
is constructed. Then, a back-transformation on the confidence limits yields an asymmetric confidence interval for  . Applying the results of Browne (1982), a (1
. Applying the results of Browne (1982), a (1 )100% confidence interval for the orthogonal factor loading
)100% confidence interval for the orthogonal factor loading  is
is
 |
where
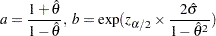 |
and  is the estimated factor loading,
is the estimated factor loading,  is the standard error estimate of the factor loading, and
is the standard error estimate of the factor loading, and 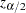 is the
is the 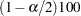 percentile point of a standard normal distribution.
percentile point of a standard normal distribution.
Once the confidence limits are constructed, you can use the corresponding coverage displays for determining the salience of the variable-factor relationship. In a coverage display, the COVER= value is represented by an asterisk (*). The following table summarizes various displays and their interpretations.
Positive Estimate |
Negative Estimate |
COVER=0 Specified |
Interpretation |
|---|---|---|---|
[0]* |
*[0] |
The estimate is not significantly different from zero, and the CI covers a region of values that are smaller in magnitude than the COVER |
|
0[ ]* |
*[ ]0 |
The estimate is significantly different from zero, but the CI covers a region of values that are smaller in magnitude than the COVER |
|
[0*] |
[*0] |
[0] |
The estimate is not significantly different from zero or the COVER |
0[*] |
[*]0 |
The estimate is significantly different from zero but not from the COVER |
|
0*[ ] |
[ ]*0 |
0[ ] or [ ]0 |
The estimate is significantly different from zero, and the CI covers a region of values that are larger in magnitude than the COVER |
See Example 33.4 for an illustration of the use of confidence intervals for interpreting factors.
Copyright © SAS Institute, Inc. All Rights Reserved.
 value. This is strong statistical evidence for the nonsalience of the variable-factor relationship.
value. This is strong statistical evidence for the nonsalience of the variable-factor relationship.