The Power and Sample Size Application: The Example

The Power and Sample Size Application

The Example

Suppose you are interested in testing how two experimental drugs affect systolic blood pressure relative to a standard drug. You want to include both men and women in the study. You have a two-factor design: a drug factor with three levels and a gender factor with two levels. You choose a main-effects-only model because you do not expect a drug by gender interaction. You want to calculate the sample size that will produce a power of 0.9 using a significance level of 0.05. You believe that the error standard deviation is between 5 and 7 mm pressure. This is a two-way analysis of variance, so the general linear univariate models task is the appropriate one.

Editing Properties

Start by opening the New window (File $\text{[math]}$ New). In the Analysis of Variance and Linear models section of the New window, select General linear univariate models. The General univariate linear models project appears, with the Edit Properties page displayed.

Project Description

For the example, change the project description to Three blood pressure drugs and gender.

Solve For

Click the Solve For tab and select the Sample size option.

Variables

Click the Variables tab to enter the names of the factors in the design. Click the Add button. The Factor Definition window appears, as shown in Figure 69.60.

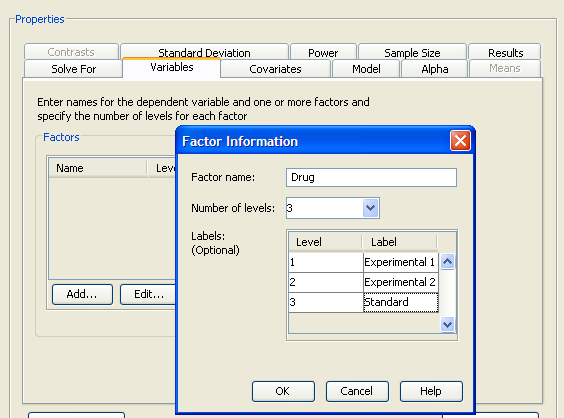
Figure 69.60 Factor Definition Window

Enter the name for the first factor, Drug, and enter the number of factor levels in the Number of levels: list box. There are three levels for this factor. Optionally, you can provide a label for each factor level. This label is used to identify factor levels on other tabs of the Edit Properties page. For this example enter the labels Experimental 1, Experimental 2, and Standard for the three levels of the Drug factor. Click OK when you are finished.

Click the Add button again and repeat the process for the second factor, Gender with two levels and labels Female and Male.

Factors can contain blanks and other special characters. Do not use an asterisk (*) because a factor name with an asterisk might be confused with an interaction effect. Factor names can be any length, but they must be distinct from one another in the first 32 characters.

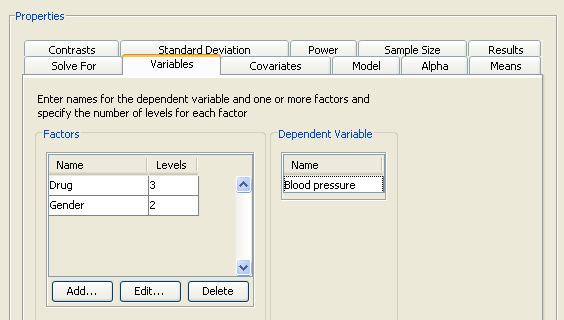
On the Variables tab, you can also specify the name of the dependent variable; in this example, Blood pressure is used.

The completed Variables tab is shown in Figure 69.61.

Figure 69.61 Variables Tab with Factors and Number of Levels

Model

Click the Model tab, then choose from three model options:

Main effects: Only the main effects are included in the model.
Main effects and all interactions: The main effects and all possible interactions are included in the model.
Custom model: Selected effects are included in the model. The effects are selected in a model builder that is displayed when this model is selected. For more information about specifying a custom model, see the section Specifying a Custom Model.

For this example, choose the default Main effects model, as shown in Figure 69.62.

Figure 69.62 Model Tab with Main Effects Selected

Alpha

Click the Alpha tab to specify one or more significance levels. For the example, specify a single significance level of 0.05.

Alpha is the significance level (that is, the probability of falsely rejecting the null hypothesis). If you frequently use the same values for alpha, set them as the defaults in the Preferences window (Tools $\text{[math]}$ Preferences).

Means

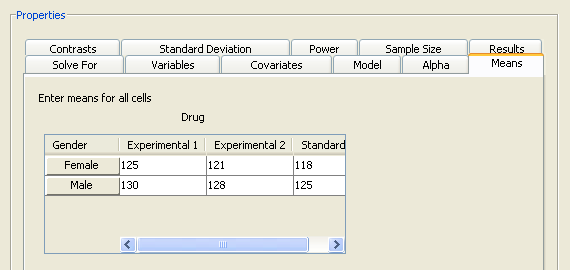
Click the Means tab to enter projected cell means for each cell of the design. The completed means for the example are shown in Figure 69.63.

Figure 69.63 Means Tab with Cell Means

Standard Deviation

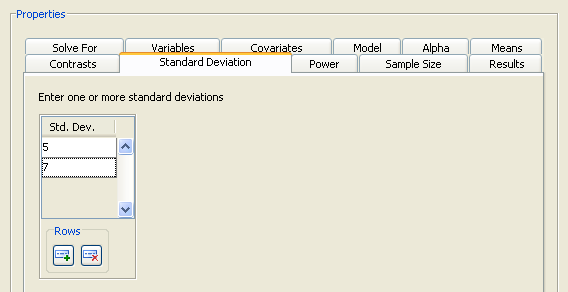
Click the Standard Deviation tab to specify one or more conjectured error standard deviations. The standard deviation is the same as the root mean squared error. For this example, enter two standard deviations, 5 and 7, as shown in Figure 69.64.

Figure 69.64 Standard Deviations Tab

Relative Sample Size

Click the Sample Size tab to select whether cell sample sizes are equal or unequal.

Figure 69.65 Sample Size Tab with Equal Cell Sample Sizes

For the example, select the Equal cell sizes option, as shown in Figure 69.65.

When solving for sample size, it is necessary to specify whether the cell sample sizes are equal or unequal. If cell sizes are unequal, relative sample size weights must also be specified. For more information about providing sample size weights, see the section Using Unequal Cell Sizes.

Power

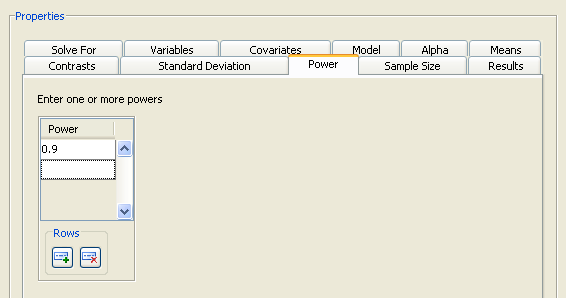
Click the Power tab to specify one or more powers. For this example, enter a single power of 0.9, as shown in Figure 69.66.

Figure 69.66 Power Tab

Summary of Input Parameters

Table 69.6 contains the values of the input parameters for the example.

Table 69.6 Summary of Input Parameters
Parameter	Value
Model	Main effects
Alpha	0.05
Means	See Table 69.7
Standard deviation	5, 7
Relative sample sizes	Equal cell sizes
Power	0.9

Table 69.7 Cell Means
Gender	Experimental 1	Experimental 2	Standard
	Drug
Female	125	121	118
Male	130	128	125

Results Options

Click the Results tab to select desired results. For the example, select both the Create summary table and Create power by sample size graph check boxes.

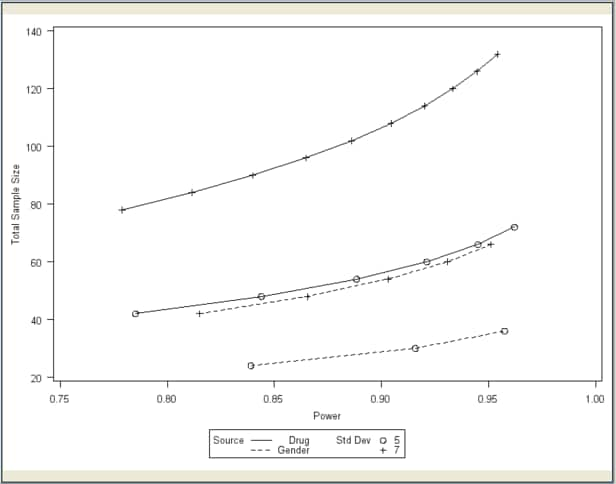
The graph consists of four points, one for each of the four scenarios that were created by combining the two factor main effects with the two standard deviations. This graph is not very informative, so specify a range of powers for the horizontal power axis. To change the power axis of the graph, click the Customize button beside the Create power by sample size graph check box to open the Customize Graph window.

Figure 69.67 Value Ranges on Customize Graph Window

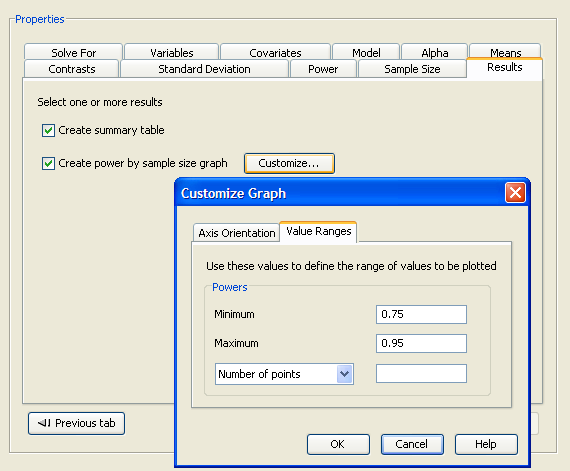
Click the Value Ranges tab and enter a minimum power of 0.75 and a maximum power of 0.95, as shown in Figure 69.67. Click OK to close the window.

Now, click Calculate to perform the analysis.

Viewing Results

The results are displayed in separate tabs on the View Results page.

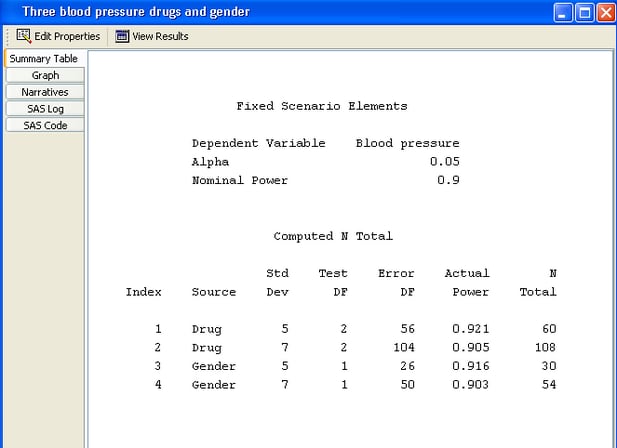
Click the Summary Table tab to view the summary table. In the Computed N Total table, sample sizes are listed for each combination of factor and standard deviation (Figure 69.68). You need a total sample size between 60 and 108 to yield a power of 0.9 for the Drug effect if the standard deviation is between 5 and 7. You need a sample size of half that for the Gender effect.

Figure 69.68 Summary Table

Click the Graph tab to view the power by sample size graph, as shown in Figure 69.69. One approximately linear curve is displayed for each standard deviation and factor combination.

Figure 69.69 Power by Sample Size Graph

Click the Narratives tab to create narratives of one or more scenarios. Select the first scenario, the Drug effect with the standard deviation of 5, in the narrative selector table. Note that the cell means are not included in the following narrative description:

For the usual F test of the Drug effect in the general linear univariate model with fixed class effects [Blood pressure = Drug Gender] using a significance level of 0.05, assuming the specified cell means and an error standard deviation of 5, a total sample size of 60 assuming a balanced design is required to obtain a power of at least 0.9. The actual power is 0.921.

For more information about using the narrative facility, see the section Creating Narratives.

Top of Page