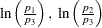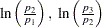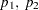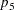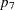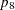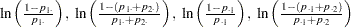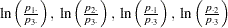| The CATMOD Procedure |
| RESPONSE Statement |
The RESPONSE statement specifies functions of the response probabilities. The procedure models these response functions as linear combinations of the parameters.
By default, PROC CATMOD uses the standard response functions (generalized logits, which are explained in detail in the section Understanding the Standard Response Functions). With these standard response functions, the default estimation method is maximum likelihood, but you can use the WLS option in the MODEL statement to request weighted least squares estimation. With other response functions (specified in the RESPONSE statement), the default (and only) estimation method is weighted least squares.
You can specify more than one RESPONSE statement, in which case each RESPONSE statement produces a separate analysis. If the computed response functions for any population are linearly dependent (yielding a singular covariance matrix), then PROC CATMOD displays an error message and stops processing. See the section Cautions for methods of dealing with this.
The function specification can be any of the items in the following list. For an example of response functions generated and formulas for 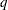 (the number of response functions), see the section More on Response Functions.
(the number of response functions), see the section More on Response Functions.
- ALOGIT
- ALOGITS
specifies response functions as adjacent-category logits of the marginal probabilities for each of the dependent variables. For each dependent variable, the response functions are a set of linearly independent adjacent-category logits, obtained by taking the logarithms of the ratios of two probabilities. The denominator of the
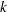 th ratio is the marginal probability corresponding to the
th ratio is the marginal probability corresponding to the 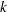 th level of the variable, and the numerator is the marginal probability corresponding to the (
th level of the variable, and the numerator is the marginal probability corresponding to the ( )th level. If a dependent variable has two levels, then the adjacent-category logit is the negative of the generalized logit.
)th level. If a dependent variable has two levels, then the adjacent-category logit is the negative of the generalized logit. - CLOGIT
- CLOGITS
specifies that the response functions are cumulative logits of the marginal probabilities for each of the dependent variables. For each dependent variable, the response functions are a set of linearly independent cumulative logits, obtained by taking the logarithms of the ratios of two probabilities. The denominator of the
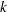 th ratio is the cumulative probability,
th ratio is the cumulative probability,  , corresponding to the
, corresponding to the 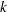 th level of the variable, and the numerator is
th level of the variable, and the numerator is  (Agresti; 1984, 113–114). If a dependent variable has two levels, then PROC CATMOD computes its cumulative logit as the negative of its generalized logit. You should use cumulative logits only when the dependent variables are ordinally scaled.
(Agresti; 1984, 113–114). If a dependent variable has two levels, then PROC CATMOD computes its cumulative logit as the negative of its generalized logit. You should use cumulative logits only when the dependent variables are ordinally scaled. - JOINT
specifies that the response functions are the joint response probabilities. A linearly independent set is created by deleting the last response probability. For the case of one dependent variable, the JOINT and MARGINALS specifications are equivalent.
- LOGIT
- LOGITS
specifies that the response functions are generalized logits of the marginal probabilities for each of the dependent variables. For each dependent variable, the response functions are a set of linearly independent generalized logits, obtained by taking the logarithms of the ratios of two probabilities. The denominator of each ratio is the marginal probability corresponding to the last observed level of the variable, and the numerators are the marginal probabilities corresponding to each of the other levels. If there is one dependent variable, then specifying LOGIT is equivalent to using the standard response functions.
- MARGINAL
- MARGINALS
specifies that the response functions are marginal probabilities for each of the dependent variables in the MODEL statement. For each dependent variable, the response functions are a set of linearly independent marginals, obtained by deleting the marginal probability corresponding to the last level.
- MEAN
- MEANS
specifies that the response functions are the means of the dependent variables in the MODEL statement. This specification requires that all of the dependent variables be numeric.
- READ variables
specifies that the response functions and their covariance matrix are to be read directly from the input data set with one response function for each variable named. See the section Inputting Response Functions and Covariances Directly for more information.
- transformation
specifies response functions that can be expressed by using successive applications of the four operations:
 ,
,  ,
,  matrix literal, or
matrix literal, or 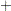 matrix literal. The operations are described in detail in the section Using a Transformation to Specify Response Functions.
matrix literal. The operations are described in detail in the section Using a Transformation to Specify Response Functions.
You can specify the following options in the RESPONSE statement after a slash.
- OUT=SAS-data-set
produces a SAS data set that contains, for each population, the observed and predicted values of the response functions, their standard errors, and the residuals. Moreover, if you use the standard response functions, the data set also includes observed and predicted values of the cell frequencies or the cell probabilities. For further information, see the section Output Data Sets.
- OUTEST=SAS-data-set
produces a SAS data set that contains the estimated parameter vector and its estimated covariance matrix. For further information, see the section Output Data Sets.
- TITLE=’title’
displays the title at the top of certain pages of output that correspond to this RESPONSE statement.
More on Response Functions
Suppose the dependent variable A has three levels and is the only response-effect in the MODEL statement. The following table shows the proportions upon which the response functions are defined:
Value of A: |
1 |
2 |
3 |
|---|---|---|---|
Proportions: |
|
|
|
Note that  . The following table shows the response functions generated for each population:
. The following table shows the response functions generated for each population:
Function |
Value |
|
|---|---|---|
Specification |
of |
Response Function |
none |
2 |
|
ALOGITS |
2 |
|
CLOGITS |
2 |
|
JOINT |
2 |
|
LOGITS |
2 |
|
MARGINAL |
2 |
|
MEAN |
1 |
|
|
||
Now, suppose the dependent variables A and B each have three levels (valued 1, 2, and 3 each) and the response-effect in the MODEL statement is A*B. The following table shows the proportions upon which the response functions are defined:
Value of A: |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
|---|---|---|---|---|---|---|---|---|---|
Value of B: |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
Proportions: |
|
|
|
|
|
|
|
|
|
The marginal totals for the preceding table are defined as follows:
 |
where  . The following table shows the response functions generated for each population:
. The following table shows the response functions generated for each population:
Function |
Value |
|
|---|---|---|
Specification |
of |
Response Function |
none |
8 |
|
ALOGITS |
4 |
|
CLOGITS |
4 |
|
JOINT |
8 |
|
LOGITS |
4 |
|
MARGINAL |
4 |
|
MEAN |
2 |
|
|
||
The READ and transformation function specifications are not shown in the preceding table. For these two situations, there is not a general response function; the response functions that are generated depend on what you specify.
Another important aspect of the function specification is the number of response functions generated per population, 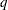 . Let
. Let  represent the number of levels for the
represent the number of levels for the 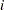 th dependent variable in the MODEL statement, and let
th dependent variable in the MODEL statement, and let 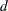 represent the number of dependent variables in the MODEL statement. Then, if the function specification is ALOGITS, CLOGITS, LOGITS, or MARGINALS, the number of response functions is
represent the number of dependent variables in the MODEL statement. Then, if the function specification is ALOGITS, CLOGITS, LOGITS, or MARGINALS, the number of response functions is
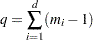 |
If the function specification is JOINT or the default (generalized logits), the number of response functions per population is
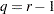 |
where  is the number of response profiles. If every possible cross-classification of the dependent variables is observed in the samples, then
is the number of response profiles. If every possible cross-classification of the dependent variables is observed in the samples, then
 |
Otherwise,  is the number of cross-classifications actually observed.
is the number of cross-classifications actually observed.
If the function specification is MEANS, the number of response functions per population is  .
.
Response Statement Examples
Some example response statements are shown in the following table:
Example |
Result |
|---|---|
response marginals; |
Marginals for each dependent variable |
response means; |
The mean of each dependent variable |
response logits; |
Generalized logits of the marginal probabilities |
response clogits; |
Cumulative logits of the marginal probabilities |
response alogits; |
Adjacent-category logits of the marginal probabilities |
response joint; |
The joint probabilities |
response 1 -1 log; |
The logit |
response; |
Generalized logits |
response 1 2 3; |
The mean score, with scores of 1, 2, and 3 corresponding to the three response levels |
response read b1-b4; |
Four response functions and their covariance matrix, read directly from the input data set |
Using a Transformation to Specify Response Functions
If you specify a transformation, it is applied to the vector that contains the sample proportions in each population. The transformation can be any combination of the following four operations:
Operation |
Specification |
|---|---|
linear combination |
|
linear combination |
matrix literal |
logarithm |
|
exponential |
|
adding constant |
|
If more than one operation is specified, then PROC CATMOD applies the operations consecutively from right to left.
A matrix literal is a matrix of numbers with each row of the matrix separated from the next by a comma. If you specify a linear combination, in most cases the  is not needed. The following statement defines the response function
is not needed. The following statement defines the response function 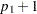 . The
. The  is needed to separate the two matrix literals '1' and '1 0'.
is needed to separate the two matrix literals '1' and '1 0'.
response + 1 * 1 0;
The  of a vector transforms each element of the vector into its natural logarithm; the
of a vector transforms each element of the vector into its natural logarithm; the  of a vector transforms each element into its exponential function (antilogarithm).
of a vector transforms each element into its exponential function (antilogarithm).
In order to specify a linear response function for data that have  response categories, you can specify either of the following RESPONSE statements:
response categories, you can specify either of the following RESPONSE statements:
response * 1 0 0 , 0 1 0; response 1 0 0 , 0 1 0;
The matrix literal in the preceding statements specifies a 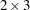 matrix, which is applied to each population as follows:
matrix, which is applied to each population as follows:
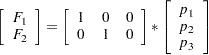 |
where  ,
, 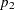 , and
, and  are sample proportions for the three response categories in a population, and
are sample proportions for the three response categories in a population, and 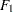 and
and  are the two response functions computed for that population. Therefore, this response function sets
are the two response functions computed for that population. Therefore, this response function sets 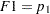 and
and  in each population.
in each population.
As another example of the linear response function, suppose you have two dependent variables corresponding to two observers who evaluate the same subjects. If the observers grade on the same three-point scale and if all nine possible responses are observed, then the following RESPONSE statement would compute the probability that the observers agree on their assessments:
response 1 0 0 0 1 0 0 0 1;
This response function is then computed as
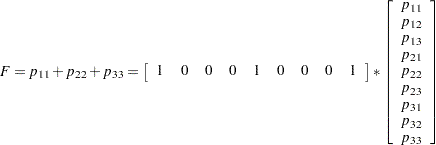 |
where 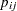 denotes the probability that a subject gets a grade of
denotes the probability that a subject gets a grade of 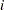 from the first observer and
from the first observer and 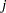 from the second observer.
from the second observer.
If the function is a compound function, requiring more than one operation to specify it, then the operations should be listed so that the first operation to be applied is on the right and the last operation to be applied is on the left. For example, if there are two response levels, you can have the following response function:
response 1 -1 log;
This is equivalent to the matrix expression
 |
which is the logit response function since 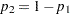 when there are only two response levels.
when there are only two response levels.
The following statement specifies another example of a compound response function:
response exp 1 -1 * 1 0 0 1, 0 1 1 0 log;
This is equivalent to the matrix expression
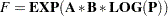 |
where 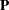 is the vector of sample proportions for some population,
is the vector of sample proportions for some population,
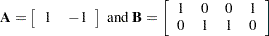 |
If the four responses are based on two dependent variables, each with two levels, then the function can also be written as
 |
which is the odds (crossproduct) ratio for a  table.
table.
Understanding the Standard Response Functions
If no RESPONSE statement is specified, PROC CATMOD computes the standard response functions, which contrast the log of each response probability with the log of the probability for the last response category. If there are  response categories, then there are
response categories, then there are 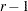 standard response functions. For example, if there are four response categories, using no RESPONSE statement is equivalent to specifying the following:
standard response functions. For example, if there are four response categories, using no RESPONSE statement is equivalent to specifying the following:
response 1 0 0 -1,
0 1 0 -1,
0 0 1 -1 log;
This results in three response functions:
 |
If there are only two response levels, the resulting response function would be a logit, which is why the standard response functions are called generalized logits. They are useful in dealing with the log-linear model:
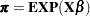 |
If 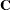 denotes the matrix in the preceding RESPONSE statement, then because of the restriction that the probabilities sum to 1, it follows that an equivalent model is
denotes the matrix in the preceding RESPONSE statement, then because of the restriction that the probabilities sum to 1, it follows that an equivalent model is
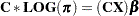 |
But  is simply the vector of standard response functions. Thus, fitting a log-linear model on the cell probabilities is equivalent to fitting a linear model on the generalized logits.
is simply the vector of standard response functions. Thus, fitting a log-linear model on the cell probabilities is equivalent to fitting a linear model on the generalized logits.
Copyright © SAS Institute, Inc. All Rights Reserved.