Example 25.14 Comparing the ML and FIML Estimation
This example uses the complete data set from Example 25.11 to illustrate how the maximum likelihood (ML) and full information maximum likelihood (FIML) methods are theoretically equivalent when you apply them to data set without missing values. In Example 25.13, you apply a confirmatory factor model to a data set with missing values. You find that with METHOD=FIML, you can get more stable estimates than with METHOD=ML (which is the default estimation method). Near the end of Example 25.13, you learn that ML and FIML are theoretically equivalent estimation methods when you apply them to data sets without missing values.
However, the ML and FIML methods have two major computational differences in their implementations in PROC CALIS. First, with METHOD=FIML the first-order properties (that is, the means of the variables) of the data are automatically included in the analysis. However, by default you analyze only the second-order properties (that is, the covariances of the variables) with METHOD=ML. Second, the biased sample covariance formula (with N as the variance divisor) is used with METHOD=FIML, while the unbiased sample covariance formula (with DF=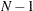 as the variance divisor) is used with METHOD=ML. See the section Relationships among Estimation Criteria for more details about the similarities and differences between the ML and FIML methods.
as the variance divisor) is used with METHOD=ML. See the section Relationships among Estimation Criteria for more details about the similarities and differences between the ML and FIML methods.
If you take care of these two differences between ML and FIML in PROC CALIS, you can obtain exactly the same results with these two methods when you apply them to data sets without missing values.
For example, with the complete data set scores from Example 25.11, you specify the FIML estimation in the following statements:
proc calis method=fiml data=scores;
factor
verbal ---> x1-x3,
math ---> y1-y3;
pvar
verbal = 1.,
math = 1.;
run;
An equivalent specification with the ML method is shown in the following statements:
proc calis method=ml meanstr vardef=n data=scores;
factor
verbal ---> x1-x3,
math ---> y1-y3;
pvar
verbal = 1.,
math = 1.;
run;
In the PROC CALIS statement, you specify two options to make the ML estimation exactly equivalent to the FIML estimation in PROC CALIS. First, the MEANSTR option requests the first-order properties (the mean structures) to be analyzed with the covariance structures. Second, the VARDEF=N option defines the variance divisor to N, instead of the default DF, which is the same as N 1. These two options make the ML estimation equivalent to the FIML estimation.
1. These two options make the ML estimation equivalent to the FIML estimation.
Output 25.14.1 and Output 25.14.2 show some fit summary statistics under the FIML and ML methods, respectively.
Output 25.14.1
Model Fitting by the FIML Method: Scores Data
| 31.7837 |
| 10.1215 |
| 8 |
| 0.2566 |
| 0.0504 |
| 0.0910 |
| 0.9872 |
Output 25.14.2
Model Fitting by the ML Method: Scores Data
| 0.3163 |
| 10.1215 |
| 8 |
| 0.2566 |
| 0.0504 |
| 0.0910 |
| 0.9872 |
Except for the fit function values, both FIML and ML methods produce the same set of fit statistics. The difference in the fit function values is expected because the FIML function has a constant term which is derived from the likelihood function. This constant term does not depend on the model parameters. Hence, the FIML and ML discrepancy functions that are used in PROC CALIS are equivalent when VARDEF=N is used in the ML method for analyzing mean and covariance structures.
The parameter estimates are shown in Output 25.14.3 and Output 25.14.4 for the FIML and ML methods, respectively. Except for very tiny numerical differences in some estimates, the FIML and ML estimates match.
Output 25.14.3
Parameter Estimates by the FIML Method: Scores Data
| 5.7486 |
| 0.9651 |
| 5.9567 |
| [_Parm1] |
|
|
| 5.7265 |
| 0.9239 |
| 6.1980 |
| [_Parm2] |
|
|
| 4.5886 |
| 0.7570 |
| 6.0618 |
| [_Parm3] |
|
|
|
| 5.1972 |
| 0.6779 |
| 7.6662 |
| [_Parm4] |
|
|
| 4.1342 |
| 0.6025 |
| 6.8612 |
| [_Parm5] |
|
|
| 3.7004 |
| 0.6143 |
| 6.0237 |
| [_Parm6] |
|
|
| 0.5175 |
| 0.1406 |
| 3.6804 |
| [_Add01] |
|
| 0.5175 |
| 0.1406 |
| 3.6804 |
| [_Add01] |
|
|
| _Add02 |
19.90625 |
1.17540 |
16.93575 |
| _Add03 |
18.81250 |
1.14089 |
16.48928 |
| _Add04 |
18.68750 |
0.92749 |
20.14856 |
| _Add05 |
17.90625 |
0.93161 |
19.22084 |
| _Add06 |
17.84375 |
0.78823 |
22.63773 |
| _Add07 |
17.75000 |
0.76419 |
23.22725 |
| _Add08 |
11.16406 |
4.06574 |
2.74589 |
| _Add09 |
8.85978 |
3.65403 |
2.42466 |
| _Add10 |
6.47248 |
2.47685 |
2.61319 |
| _Add11 |
0.76135 |
1.23420 |
0.61687 |
| _Add12 |
2.79060 |
1.04306 |
2.67539 |
| _Add13 |
4.99466 |
1.40025 |
3.56698 |
Output 25.14.4
Parameter Estimates by the ML Method: Scores Data
| 5.7486 |
| 0.9651 |
| 5.9567 |
| [_Parm1] |
|
|
| 5.7265 |
| 0.9239 |
| 6.1981 |
| [_Parm2] |
|
|
| 4.5885 |
| 0.7570 |
| 6.0617 |
| [_Parm3] |
|
|
|
| 5.1972 |
| 0.6779 |
| 7.6662 |
| [_Parm4] |
|
|
| 4.1341 |
| 0.6025 |
| 6.8612 |
| [_Parm5] |
|
|
| 3.7004 |
| 0.6143 |
| 6.0238 |
| [_Parm6] |
|
|
| 0.5175 |
| 0.1406 |
| 3.6800 |
| [_Add01] |
|
| 0.5175 |
| 0.1406 |
| 3.6800 |
| [_Add01] |
|
|
| _Add02 |
19.90625 |
1.17540 |
16.93575 |
| _Add03 |
18.81250 |
1.14089 |
16.48928 |
| _Add04 |
18.68750 |
0.92749 |
20.14856 |
| _Add05 |
17.90625 |
0.93161 |
19.22084 |
| _Add06 |
17.84375 |
0.78823 |
22.63773 |
| _Add07 |
17.75000 |
0.76419 |
23.22725 |
| _Add08 |
11.16365 |
4.06567 |
2.74583 |
| _Add09 |
8.85925 |
3.65397 |
2.42456 |
| _Add10 |
6.47288 |
2.47689 |
2.61331 |
| _Add11 |
0.76124 |
1.23420 |
0.61679 |
| _Add12 |
2.79066 |
1.04307 |
2.67543 |
| _Add13 |
4.99461 |
1.40024 |
3.56697 |
The equivalence between METHOD=ML and METHOD=FIML implies that if you do not have any missing data in your data, you can just use METHOD=ML because it is computationally more efficient than the FIML method.
While the equivalence between ML and FIML is established here with the use of the VARDEF= and MEANSTR options (for data without missing values), it is not necessary in practice to use these options with METHOD=ML. The VARDEF= option is used in this example only to demonstrate the theoretical equivalence between METHOD=ML and METHOD=FIML. The VARDEF= option has very little effect if you have at least a moderate sample size (for example, 30 or more observations).
Merely adding the MEANSTR option to an analysis for data without missing values amounts to adding a saturated mean structure to a covariance structure analysis. In this case, the MEANSTR option only gives you more estimates that pertain to the mean structures, but the parameter estimates that pertain to the covariance structures do not change. Therefore, use the MEANSTR option only when you need to estimate certain mean structure parameters or when you fit models with nonsaturated mean structures.
However, use METHOD=FIML when there are missing values in your data and you need to use every bit of information from the incomplete observations with random missing values.
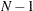 as the variance divisor) is used with METHOD=ML. See the section Relationships among Estimation Criteria for more details about the similarities and differences between the ML and FIML methods.
as the variance divisor) is used with METHOD=ML. See the section Relationships among Estimation Criteria for more details about the similarities and differences between the ML and FIML methods.  1. These two options make the ML estimation equivalent to the FIML estimation.
1. These two options make the ML estimation equivalent to the FIML estimation.