| The TCALIS Procedure |
Example 88.1 Path Analysis: Stability of Alienation
The following covariance matrix from Wheaton et al. (1977) has served to illustrate the performance of several implementations for the analysis of structural equation models. Two different models have been analyzed by an early implementation of LISREL and are mentioned in Jöreskog (1978). You can also find a more detailed discussion of these models in the LISREL VI manual (Jöreskog and Sörbom 1985). A slightly modified model for this covariance matrix is included in the EQS 2.0 manual (Bentler 1985, p. 28). The path diagram of this model is displayed in Figure 88.2. The same model is reanalyzed here by PROC TCALIS. However, for the analysis with the EQS implementation, the SEI variable is rescaled by a factor of 0.1 to make the matrix less ill-conditioned. Since the Levenberg-Marquardt or Newton-Raphson optimization techniques are used with PROC CALIS, rescaling the data matrix is not necessary and, therefore, is not done here. The results reported here reflect the estimates based on the original covariance matrix.
title "Stability of Alienation";
title2 "Data Matrix of WHEATON, MUTHEN, ALWIN & SUMMERS (1977)";
data Wheaton(TYPE=COV);
_type_ = 'cov';
input _name_ $ 1-11 Anomie67 Powerless67 Anomie71 Powerless71
Education SEI;
label Anomie67='Anomie (1967)' Powerless67='Powerlessness (1967)'
Anomie71='Anomie (1971)' Powerless71='Powerlessness (1971)'
Education='Education' SEI='Occupational Status Index';
datalines;
Anomie67 11.834 . . . . .
Powerless67 6.947 9.364 . . . .
Anomie71 6.819 5.091 12.532 . . .
Powerless71 4.783 5.028 7.495 9.986 . .
Education -3.839 -3.889 -3.841 -3.625 9.610 .
SEI -21.899 -18.831 -21.748 -18.775 35.522 450.288
;
ods graphics on;
proc tcalis nobs=932 data=Wheaton plots=residuals;
path
Anomie67 <- Alien67 1.0,
Powerless67 <- Alien67 0.833,
Anomie71 <- Alien71 1.0,
Powerless71 <- Alien71 0.833,
Education <- SES 1.0,
SEI <- SES lambda,
Alien67 <- SES gamma1,
Alien71 <- SES gamma2,
Alien71 <- Alien67 beta;
pvar
Anomie67 = theta1,
Powerless67 = theta2,
Anomie71 = theta1,
Powerless71 = theta2,
Education = theta3,
SEI = theta4,
Alien67 = psi1,
Alien71 = psi2,
SES = phi;
pcov
Anomie67 Anomie71 = theta5,
Powerless67 Powerless71 = theta5;
run;
ods graphics off;
Since no METHOD= option has been used, maximum likelihood estimates are computed by default. In this example, no global display options are specified. This means that PROC TCALIS prints the default set of results.
PROC TCALIS can produce a high-quality residual histogram that is useful for showing the distribution of residuals. To request the residual histogram, you must first enable ODS Graphics by specifying the ods graphics on statement, as shown in the preceding statements before the PROC TCALIS statement. Then, the residual histogram is requested by the plots=residuals option in the PROC TCALIS statement.
Output 88.1.1 displays the modeling information and variables in the analysis.
| Modeling Information | |
|---|---|
| Data Set | WORK.WHEATON |
| N Obs | 932 |
| Model Type | PATH |
Output 88.1.1 shows that the data set Wheaton was used with 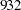 observations. The model is specified with the PATH modeling language. Variables in the model are classified into different categories according to their roles. All manifest variables are endogenous in the model. Also, three latent variables are hypothesized in the model: Alien67, Alien71, and SES. While Alien67 and Alien71 are endogenous, SES is exogenous in the model.
observations. The model is specified with the PATH modeling language. Variables in the model are classified into different categories according to their roles. All manifest variables are endogenous in the model. Also, three latent variables are hypothesized in the model: Alien67, Alien71, and SES. While Alien67 and Alien71 are endogenous, SES is exogenous in the model.
Output 88.1.2 echoes the initial specification of the PATH model.
| Initial Estimates for PATH List | ||||
|---|---|---|---|---|
| Path | Parameter | Estimate | ||
| Anomie67 | <- | Alien67 | 1.00000 | |
| Powerless67 | <- | Alien67 | 0.83300 | |
| Anomie71 | <- | Alien71 | 1.00000 | |
| Powerless71 | <- | Alien71 | 0.83300 | |
| Education | <- | SES | 1.00000 | |
| SEI | <- | SES | lambda | . |
| Alien67 | <- | SES | gamma1 | . |
| Alien71 | <- | SES | gamma2 | . |
| Alien71 | <- | Alien67 | beta | . |
In Output 88.1.2, numerical values for estimates are the initial values you input in the model specification. If the associated parameter name for a numerical estimate is blank, it means that the estimate is a fixed value, which would not be changed in the estimation. For example, the first five paths have fixed path coefficients with the fixed values given. For numerical estimates with parameter names given, the numerical values serve as initial values, which would be changed during the estimation. In Output 88.1.2, you actually do not have this kind of specification. All free parameters specified in the model are with missing initial values, denoted by '.'. For example, lambda, gamma1, theta1, and psi1, among others, are free parameters without initial values given. The initial values of these parameters will be generated by PROC TCALIS automatically.
You can examine this output to ensure that the desired model is being analyzed. PROC TCALIS outputs the initial specifications or the estimation results in the order you specify in the model, unless you use reordering options such as ORDERSPEC and ORDERALL. Therefore, the input order of specifications is important—it determines how your output would look.
Simple descriptive statistics are displayed in Output 88.1.3.
Initial estimates are necessary in all kinds of optimization problems. They could be provided by users or automatically generated by PROC TCALIS. As shown in Output 88.1.2, you did not provide any initial estimates for all free parameters. PROC TCALIS uses a combination of well-behaved mathematical methods to complete the initial estimation. The initial estimation methods for the current analysis are shown in Output 88.1.4.
| Initial Estimation Methods | |
|---|---|
| 1 | Instrumental Variables Method |
| 2 | McDonald Method |
| 3 | Two-Stage Least Squares |
| Optimization Start Parameter Estimates |
|||
|---|---|---|---|
| N | Parameter | Estimate | Gradient |
| 1 | lambda | 4.99508 | -0.00206 |
| 2 | gamma1 | -0.62322 | -0.04069 |
| 3 | gamma2 | -0.20437 | -0.03816 |
| 4 | beta | 0.66589 | 0.03789 |
| 5 | theta1 | 3.51433 | -0.00409 |
| 6 | theta2 | 3.65991 | 0.01182 |
| 7 | theta3 | 2.49860 | -0.00578 |
| 8 | theta4 | 272.85274 | 0.0000194 |
| 9 | psi1 | 5.57764 | -0.00217 |
| 10 | psi2 | 3.79636 | -0.00935 |
| 11 | phi | 7.11140 | 0.00108 |
| 12 | theta5 | 0.45298 | -0.06463 |
| Value of Objective Function = 0.0365979443 | |||
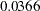 .
. Output 88.1.5 displays the optimization information, including technical details, iteration history and convergence status.
| Optimization Start | |||
|---|---|---|---|
| Active Constraints | 0 | Objective Function | 0.0365979443 |
| Max Abs Gradient Element | 0.0646338767 | Radius | 1 |
| Iteration | Restarts | Function Calls |
Active Constraints |
Objective Function |
Objective Function Change |
Max Abs Gradient Element |
Lambda | Ratio Between Actual and Predicted Change |
||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 4 | 0 | 0.01453 | 0.0221 | 0.00142 | 0 | 1.013 | ||
| 2 | 0 | 6 | 0 | 0.01448 | 0.000046 | 0.000249 | 0 | 1.001 | ||
| 3 | 0 | 8 | 0 | 0.01448 | 1.007E-7 | 4.717E-6 | 0 | 1.006 |
The convergence status is important for the validity of your solution. In most cases, you should interpret your results only when the solution is converged. In this example, you obtain a converged solution, as shown in the message at the bottom of the table. The final objective function value is 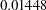 , which is the minimized function value during the optimization. If problematic solutions such as nonconvergence are encountered, PROC TCALIS issues an error message.
, which is the minimized function value during the optimization. If problematic solutions such as nonconvergence are encountered, PROC TCALIS issues an error message.
The fit summary statistics are displayed in Output 88.1.6. By default, PROC TCALIS displays all available fit indices and modeling information.
| Fit Summary | ||
|---|---|---|
| Modeling Info | N Observations | 932 |
| N Variables | 6 | |
| N Moments | 21 | |
| N Parameters | 12 | |
| N Active Constraints | 0 | |
| Independence Model Chi-Square | 2131.4327 | |
| Independence Model Chi-Square DF | 15 | |
| Absolute Index | Fit Function | 0.0145 |
| Chi-Square | 13.4851 | |
| Chi-Square DF | 9 | |
| Pr > Chi-Square | 0.1419 | |
| Z-Test of Wilson & Hilferty | 1.0754 | |
| Hoelter Critical N | 1170 | |
| Root Mean Square Residual (RMSR) | 0.2281 | |
| Standardized RMSR (SRMSR) | 0.0150 | |
| Goodness of Fit Index (GFI) | 0.9953 | |
| Parsimony Index | Adjusted GFI (AGFI) | 0.9890 |
| Parsimonious GFI | 0.5972 | |
| RMSEA Estimate | 0.0231 | |
| RMSEA Lower 90% Confidence Limit | . | |
| RMSEA Upper 90% Confidence Limit | 0.0470 | |
| Probability of Close Fit | 0.9705 | |
| ECVI Estimate | 0.0405 | |
| ECVI Lower 90% Confidence Limit | . | |
| ECVI Upper 90% Confidence Limit | 0.0556 | |
| Akaike Information Criterion | -4.5149 | |
| Bozdogan CAIC | -57.0509 | |
| Schwarz Bayesian Criterion | -48.0509 | |
| McDonald Centrality | 0.9976 | |
| Incremental Index | Bentler Comparative Fit Index | 0.9979 |
| Bentler-Bonett NFI | 0.9937 | |
| Bentler-Bonett Non-normed Index | 0.9965 | |
| Bollen Normed Index Rho1 | 0.9895 | |
| Bollen Non-normed Index Delta2 | 0.9979 | |
| James et al. Parsimonious NFI | 0.5962 | |
First, the fit summary table starts with some basic modeling information, as shown in Output 88.1.6. You can check the number of observations, number of variables, number of moments being fitted, number of parameters, number of active constraints in the solution, and the independent model chi-square and its degrees of freedom in this modeling information category. Next, three types of fit indices are shown: absolute, parsimony, and incremental.
The absolute indices are fit measures that are interpreted without referring to any baseline model and without adjusting model parsimony. The chi-square test statistic is the best-known absolute index in this category. In this example, the  -value of the chi-square is
-value of the chi-square is 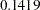 , which is larger than the conventional
, which is larger than the conventional 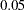 value. From a statistical hypothesis testing point of view, this model cannot be rejected. The Z-test of Wilson and Hilferty is also insignificant at
value. From a statistical hypothesis testing point of view, this model cannot be rejected. The Z-test of Wilson and Hilferty is also insignificant at 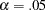 , which echoes the result of the chi-square test. Other absolute indices can also be consulted. Although it seems that there are no clear conventional levels for these indices to indicate an acceptable model fit, you can always use these indices to compare the relative fit between different models.
, which echoes the result of the chi-square test. Other absolute indices can also be consulted. Although it seems that there are no clear conventional levels for these indices to indicate an acceptable model fit, you can always use these indices to compare the relative fit between different models.
Next, the parsimony fit indices take the model parsimony into account. These indices adjust the model fit by the degrees of freedom (or the number of the parameters) of the model in certain ways. The advantage of these indices is that merely increasing the number of parameters in the model might not necessarily improve the model fit indicated by these indices. Models with large numbers of parameters are penalized. There is no uniform way to interpret all these indices. However, for the relatively well-known RMSEA estimate, by convention values under 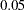 indicate good fit. The RMSEA value for this example is
indicate good fit. The RMSEA value for this example is 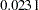 , and so this is a very good fit. For interpretations of other parsimony indices, you can consult the original articles for these indices.
, and so this is a very good fit. For interpretations of other parsimony indices, you can consult the original articles for these indices.
Last, the incremental fit indices are computed based on comparison with a baseline model, usually the independence model where all mainfest variables are assumed to be uncorrelated. The independence model fit statistic is shown under the Modeling Info category of the same fit summary table. In this example, the model fit chi-square of the independence model is 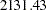 , with
, with 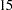 degrees of freedom. The incremental indices show how well the hypothesized model improves over the independence model for the data. Various incremental fit indices have been proposed. In the fit summary table, there are six of such fit indices. Large values for these indices are desired. It has been suggested that values larger than
degrees of freedom. The incremental indices show how well the hypothesized model improves over the independence model for the data. Various incremental fit indices have been proposed. In the fit summary table, there are six of such fit indices. Large values for these indices are desired. It has been suggested that values larger than 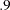 for these indices indicate acceptable model fit. In this example, all incremental indices but James et al. parsimonious NFI show that the hypothesized model fits well.
for these indices indicate acceptable model fit. In this example, all incremental indices but James et al. parsimonious NFI show that the hypothesized model fits well.
There is no consensus as to which fit index is the best to judge model fit. Probably, with artificial data and model, all fit indices can be shown defective in some aspects of measuring model fit. Conventional wisdom is to look at all fit indices and determine whether the majority of them are close to the desirable ranges of values. In this example, almost all fit indices are good, and so it is safe to conclude that the model fits well.
Nowadays, most researchers do pay less attention to the model fit chi-square statistic because it tends to reject all meaningful models with minimum departures from the truth. Although the model fit chi-square test statistic is an impeccable statistical inference tool when the underlying statistical assumptions are satisfied, for practical purposes it is just too powerful to accept any useful and reasonable models with only tiny imperfections. Some fit indices are more popular than others. Standardized RMSR, RMSEA estimate, adjusted AGFI, and Bentler’s comparative fit index are frequently reported in empirical research for judging model fit. In this example, all these measures show good model fit of the hypothesized model. While there are certainly legitimate reasons why these fit indices are more popular than others, they are out of the current scope of discussion.
PROC TCALIS can perform a detailed residual analysis. Large residuals might indicate misspecification of the model. In Output 88.1.7, raw residuals are reported and ranked.
| Raw Residual Matrix | |||||||
|---|---|---|---|---|---|---|---|
| Anomie67 | Powerless67 | Anomie71 | Powerless71 | Education | SEI | ||
| Anomie67 | Anomie (1967) | -0.06997 | 0.03642 | -0.01116 | -0.15200 | 0.32892 | 0.47786 |
| Powerless67 | Powerlessness (1967) | 0.03642 | 0.01261 | 0.15600 | 0.01135 | -0.41712 | -0.19108 |
| Anomie71 | Anomie (1971) | -0.01116 | 0.15600 | -0.08381 | -0.00854 | 0.22464 | 0.07976 |
| Powerless71 | Powerlessness (1971) | -0.15200 | 0.01135 | -0.00854 | 0.14067 | -0.23832 | -0.59248 |
| Education | Education | 0.32892 | -0.41712 | 0.22464 | -0.23832 | 0 | 4.03148E-6 |
| SEI | Occupational Status Index | 0.47786 | -0.19108 | 0.07976 | -0.59248 | 4.03148E-6 | 0.0000221 |
| Rank Order of the 10 Largest Raw Residuals | ||
|---|---|---|
| Var1 | Var2 | Residual |
| SEI | Powerless71 | -0.59248 |
| SEI | Anomie67 | 0.47786 |
| Education | Powerless67 | -0.41712 |
| Education | Anomie67 | 0.32892 |
| Education | Powerless71 | -0.23832 |
| Education | Anomie71 | 0.22464 |
| SEI | Powerless67 | -0.19108 |
| Anomie71 | Powerless67 | 0.15600 |
| Powerless71 | Anomie67 | -0.15200 |
| Powerless71 | Powerless71 | 0.14067 |
Because of the differential scaling of the variables, it is usually more useful to examine the standardized residuals instead. In Output 88.1.8, for example, the table for the 10 largest asymptotically standardized residuals is displayed.
| Asymptotically Standardized Residual Matrix | |||||||
|---|---|---|---|---|---|---|---|
| Anomie67 | Powerless67 | Anomie71 | Powerless71 | Education | SEI | ||
| Anomie67 | Anomie (1967) | -0.30882 | 0.52686 | -0.05619 | -0.86507 | 2.55338 | 0.46484 |
| Powerless67 | Powerlessness (1967) | 0.52686 | 0.05464 | 0.87613 | 0.05735 | -2.76371 | -0.17015 |
| Anomie71 | Anomie (1971) | -0.05619 | 0.87613 | -0.35460 | -0.12169 | 1.69781 | 0.07009 |
| Powerless71 | Powerlessness (1971) | -0.86507 | 0.05735 | -0.12169 | 0.58521 | -1.55750 | -0.49608 |
| Education | Education | 2.55338 | -2.76371 | 1.69781 | -1.55750 | 0 | 0 |
| SEI | Occupational Status Index | 0.46484 | -0.17015 | 0.07009 | -0.49608 | 0 | 0 |
| Rank Order of the 10 Largest Asymptotically Standardized Residuals | ||
|---|---|---|
| Var1 | Var2 | Residual |
| Education | Powerless67 | -2.76371 |
| Education | Anomie67 | 2.55338 |
| Education | Anomie71 | 1.69781 |
| Education | Powerless71 | -1.55750 |
| Anomie71 | Powerless67 | 0.87613 |
| Powerless71 | Anomie67 | -0.86507 |
| Powerless71 | Powerless71 | 0.58521 |
| Powerless67 | Anomie67 | 0.52686 |
| SEI | Powerless71 | -0.49608 |
| SEI | Anomie67 | 0.46484 |
The model performs the poorest concerning the covariances of Education with all measures of Powerless and Anomie. This might suggest a misspecification of the functional relationships of Education with other variables in the model. However, because the model fit is quite good, such a possible misspecification should not be a serious concern in the analysis.
The histogram of the asymptotically standardized residuals is displayed in Output 88.1.9, which also shows the normal and kernel approximations.
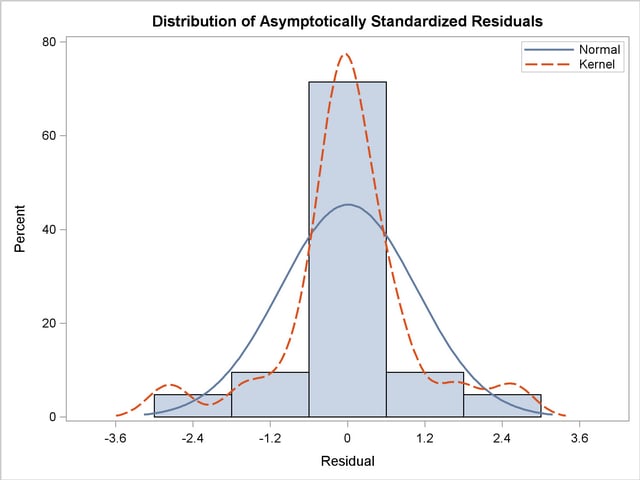
The residual distribution looks quite symmetrical. It shows a small to medium departure from the normal distribution, as evidenced by the discrepancies between the kernel and the normal distribution curves.
Estimation results are shown in Output 88.1.10.
| PATH List | ||||||
|---|---|---|---|---|---|---|
| Path | Parameter | Estimate | Standard Error |
t Value | ||
| Anomie67 | <- | Alien67 | 1.00000 | |||
| Powerless67 | <- | Alien67 | 0.83300 | |||
| Anomie71 | <- | Alien71 | 1.00000 | |||
| Powerless71 | <- | Alien71 | 0.83300 | |||
| Education | <- | SES | 1.00000 | |||
| SEI | <- | SES | lambda | 5.36883 | 0.43371 | 12.37880 |
| Alien67 | <- | SES | gamma1 | -0.62994 | 0.05634 | -11.18092 |
| Alien71 | <- | SES | gamma2 | -0.24086 | 0.05489 | -4.38836 |
| Alien71 | <- | Alien67 | beta | 0.59312 | 0.04678 | 12.67884 |
| Variance Parameters | |||||
|---|---|---|---|---|---|
| Variance Type |
Variable | Parameter | Estimate | Standard Error |
t Value |
| Error | Anomie67 | theta1 | 3.60796 | 0.20092 | 17.95717 |
| Powerless67 | theta2 | 3.59488 | 0.16448 | 21.85563 | |
| Anomie71 | theta1 | 3.60796 | 0.20092 | 17.95717 | |
| Powerless71 | theta2 | 3.59488 | 0.16448 | 21.85563 | |
| Education | theta3 | 2.99366 | 0.49861 | 6.00398 | |
| SEI | theta4 | 259.57639 | 18.31151 | 14.17559 | |
| Alien67 | psi1 | 5.67046 | 0.42301 | 13.40500 | |
| Alien71 | psi2 | 4.51479 | 0.33532 | 13.46394 | |
| Exogenous | SES | phi | 6.61634 | 0.63914 | 10.35190 |
The paths, variances and partial (or error) variances, and covariances and partial covariances are shown. When you have fixed parameters such as the first five path coefficients in the output, the standard errors and  values are all blanks. For free or constrained estimates, standard errors and
values are all blanks. For free or constrained estimates, standard errors and  values are computed. Researchers in structural equation modeling usually use the value
values are computed. Researchers in structural equation modeling usually use the value 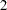 as an approximate critical value for the observed
as an approximate critical value for the observed  values. The reason is that the estimates are asymptotically normal, and so the two-sided critical point with
values. The reason is that the estimates are asymptotically normal, and so the two-sided critical point with 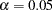 is
is 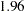 , which is close to
, which is close to 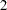 . Using this criterion, all estimates shown in Output 88.1.10 are significantly different from zero, supporting the presence of these parameters in the model.
. Using this criterion, all estimates shown in Output 88.1.10 are significantly different from zero, supporting the presence of these parameters in the model.
Squared multiple correlations are shown in Output 88.1.11.
| Squared Multiple Correlations | |||
|---|---|---|---|
| Variable | Error Variance | Total Variance | R-Square |
| Anomie67 | 3.60796 | 11.90397 | 0.6969 |
| Anomie71 | 3.60796 | 12.61581 | 0.7140 |
| Education | 2.99366 | 9.61000 | 0.6885 |
| Powerless67 | 3.59488 | 9.35139 | 0.6156 |
| Powerless71 | 3.59488 | 9.84533 | 0.6349 |
| SEI | 259.57639 | 450.28798 | 0.4235 |
| Alien67 | 5.67046 | 8.29601 | 0.3165 |
| Alien71 | 4.51479 | 9.00786 | 0.4988 |
For each endogenous variable in the model, the corresponding squared multiple correlation is computed by:
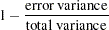 |
In regression analysis, this is the percentage of explained variance of the endogenous variable by the predictors. However, this interpretation is complicated or even uninterpretable when your structural equation model has correlated errors or reciprocal casual relations. In these situations, it is not uncommon to see negative R-squares. Negative R-squares do not necessarily mean that your model is wrong or the model prediction is weak. Rather, the R-square interpretation is questionable in these situations.
When your variables are measured on different scales, comparison of path coefficients cannot be made directly. For example, in Output 88.1.10, the path coefficient for path Education <– SES is fixed at one, while the path coefficient for path SEI <– SES is 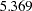 . It would be very simple-minded to conclude that the effect of SES on SEI is larger than that SES on Education. Because SEI and Education are measured on different scales, direct comparison of the corresponding path coefficients is simply inappropriate.
. It would be very simple-minded to conclude that the effect of SES on SEI is larger than that SES on Education. Because SEI and Education are measured on different scales, direct comparison of the corresponding path coefficients is simply inappropriate.
In alleviating this problem, some might resort to the standardized solution for a better comparison. In a standardized solution, because the variances of manifest variables and systematic predictors are all standardized to ones, you hope the path coefficients are more comparable. In this example, PROC TCALIS standardizes your results in Output 88.1.12.
| Standardized Results for PATH List | ||||||
|---|---|---|---|---|---|---|
| Path | Parameter | Estimate | Standard Error |
t Value | ||
| Anomie67 | <- | Alien67 | 0.83481 | 0.01093 | 76.35313 | |
| Powerless67 | <- | Alien67 | 0.78459 | 0.01163 | 67.47756 | |
| Anomie71 | <- | Alien71 | 0.84499 | 0.01031 | 81.97956 | |
| Powerless71 | <- | Alien71 | 0.79678 | 0.01107 | 71.96263 | |
| Education | <- | SES | 0.82975 | 0.03172 | 26.15990 | |
| SEI | <- | SES | lambda | 0.65079 | 0.03019 | 21.55331 |
| Alien67 | <- | SES | gamma1 | -0.56257 | 0.03456 | -16.27961 |
| Alien71 | <- | SES | gamma2 | -0.20642 | 0.04483 | -4.60430 |
| Alien71 | <- | Alien67 | beta | 0.56920 | 0.04066 | 14.00001 |
| Standardized Results for Variance Parameters | |||||
|---|---|---|---|---|---|
| Variance Type |
Variable | Parameter | Estimate | Standard Error |
t Value |
| Error | Anomie67 | theta1 | 0.30309 | 0.01825 | 16.60309 |
| Powerless67 | theta2 | 0.38442 | 0.01825 | 21.06948 | |
| Anomie71 | theta1 | 0.28599 | 0.01742 | 16.41782 | |
| Powerless71 | theta2 | 0.36514 | 0.01764 | 20.69424 | |
| Education | theta3 | 0.31152 | 0.05264 | 5.91822 | |
| SEI | theta4 | 0.57647 | 0.03930 | 14.66804 | |
| Alien67 | psi1 | 0.68352 | 0.03888 | 17.57968 | |
| Alien71 | psi2 | 0.50121 | 0.03321 | 15.08974 | |
| Exogenous | SES | phi | 1.00000 | ||
Now, the standardized path coefficient for path Education <– SES is 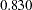 , while the standardized path coefficient for path SEI <– SES is
, while the standardized path coefficient for path SEI <– SES is 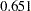 . So the standardized effect of SES on SEI is actually smaller than that of SES on Education.
. So the standardized effect of SES on SEI is actually smaller than that of SES on Education.
Furthermore, in PROC TCALIS the standardized estimates are computed with standard error estimates and  values so that you can make statistical inferences on the standardized estimates as well.
values so that you can make statistical inferences on the standardized estimates as well.
PROC TCALIS might differ from other software in its standardization scheme. Unlike other software that might standardize the path coefficients that attach to the error terms (unsystematic sources), PROC TCALIS keeps these path coefficients at ones (not shown in the output). Unlike other software that might also standardize the corresponding error variances to ones, the error variances in the standardized solution of PROC TCALIS are rescaled so as to keep the mathematical consistency of the model.
Essentially, in PROC TCALIS only variances of mainfest and non-error-type latent variables are standardized to ones. The error variances are rescaled, but not standardized. For example, in the standardized solution shown in Output 88.1.12, the error variances for all endogenous variables are not ones (see the middle portion of the output). Only the variance for the latent variable SES is standardized to one. See the section Standardized Solutions for the logic of the standardization scheme adopted by PROC TCALIS.
In appearance, the standardized solution is like a correlational analysis on the standardized manifest variables with standardized exogenous latent factors. Unfortunately, this statement is over-simplified, if not totally inappropriate. In standardizing a solution, the implicit equality constraints are likely destroyed. In this example, the unstandardized error variances for Anomie67 and Anomie71 are both 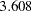 , represented by a common parameter theta1. However, after standardization, these error variances have different values at
, represented by a common parameter theta1. However, after standardization, these error variances have different values at 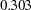 and
and 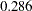 , respectively. In addition, fixed parameter values are no longer fixed in a standardized solution (for example, the first five paths in the current example). The issue of standardization is common to all other SEM software and beyond the current discussion. PROC TCALIS provides the standardized solution so that users can interpret the standardized estimates whenever they find them appropriate.
, respectively. In addition, fixed parameter values are no longer fixed in a standardized solution (for example, the first five paths in the current example). The issue of standardization is common to all other SEM software and beyond the current discussion. PROC TCALIS provides the standardized solution so that users can interpret the standardized estimates whenever they find them appropriate.
Note: This procedure is experimental.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.