| The SURVEYFREQ Procedure |
Rao-Scott Likelihood Ratio Chi-Square Test
The Rao-Scott likelihood ratio chi-square test is a design-adjusted version of the likelihood ratio test, which involves ratios between observed and expected frequencies. For two-way tables, the null hypothesis for this test is no association between the row and column variables. For one-way tables, the null hypothesis is equal proportions for the variable levels. Or you can specify null hypothesis proportions for one-way tables by using the TESTP= option.
Two forms of the design correction are available for the Rao-Scott tests. One form of the design correction uses the proportion estimates, and you request the corresponding Rao-Scott likelihood ratio test with the LRCHISQ option. The other form of the design correction uses the null hypothesis proportions. You request this test, called the Rao-Scott modified likelihood ratio test, with the LRCHISQ1 option.
See Lohr (1999), Thomas, Singh, and Roberts (1996), and Rao and Scott (1981, 1984, 1987) for details about design-adjusted chi-square tests.
Two-Way Tables
The Rao-Scott likelihood ratio statistic is computed from the likelihood ratio chi-square statistic and a design correction based on the design effects of the proportions. Under the null hypothesis of no association between the row and column variables, this statistic approximately follows a chi-square distribution with 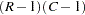 degrees of freedom. PROC SURVEYFREQ also computes an
degrees of freedom. PROC SURVEYFREQ also computes an 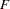 statistic that can provide a better approximation.
statistic that can provide a better approximation.
The Rao-Scott likelihood ratio chi-square 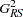 is computed as
is computed as
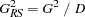 |
where 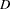 is the design correction described in the section Design Correction for Two-Way Tables, and
is the design correction described in the section Design Correction for Two-Way Tables, and 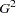 is the likelihood ratio chi-square based on the estimated totals. The likelihood ratio chi-square is computed as
is the likelihood ratio chi-square based on the estimated totals. The likelihood ratio chi-square is computed as
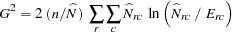 |
where  is the sample size,
is the sample size, 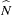 is the estimated overall total,
is the estimated overall total, 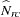 is the estimated total for table cell
is the estimated total for table cell 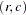 , and
, and 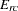 is the expected total for cell
is the expected total for cell 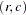 under the null hypothesis of no association. The expected total for cell
under the null hypothesis of no association. The expected total for cell 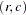 equals
equals
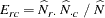 |
Under the null hypothesis of no association, the Rao-Scott likelihood ratio chi-square 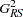 approximately follows a chi-square distribution with
approximately follows a chi-square distribution with 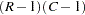 degrees of freedom. A better approximation can be obtained by the
degrees of freedom. A better approximation can be obtained by the 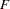 statistic,
statistic,
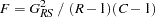 |
which has an 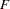 distribution with
distribution with 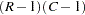 and
and 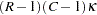 degrees of freedom under the null hypothesis. The value
degrees of freedom under the null hypothesis. The value  is the degrees of freedom for the variance estimator and depends on the sample design and the variance estimation method. The section Degrees of Freedom describes the computation of
is the degrees of freedom for the variance estimator and depends on the sample design and the variance estimation method. The section Degrees of Freedom describes the computation of  .
.
One-Way Tables
For one-way tables, the Rao-Scott likelihood ratio chi-square statistic provides a design-based goodness-of-fit test for equal proportions. Or if you specify null proportions with the TESTP= option, the Rao-Scott likelihood ratio chi-square provides a design-based goodness-of-fit test for the specified proportions. Under the null hypothesis, the Rao-Scott likelihood ratio statistic approximately follows a chi-square distribution with 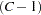 degrees of freedom for a table with
degrees of freedom for a table with  levels. PROC SURVEYFREQ also computes an
levels. PROC SURVEYFREQ also computes an 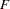 statistic that can provide a better approximation.
statistic that can provide a better approximation.
The Rao-Scott likelihood ratio chi-square 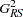 is computed as
is computed as
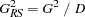 |
where 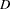 is the design correction described in the section Design Correction for One-Way Tables, and
is the design correction described in the section Design Correction for One-Way Tables, and 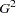 is the likelihood ratio chi-square based on the estimated totals. The likelihood ratio chi-square is computed as
is the likelihood ratio chi-square based on the estimated totals. The likelihood ratio chi-square is computed as
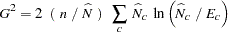 |
where  is the sample size,
is the sample size, 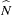 is the estimated overall total,
is the estimated overall total, 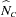 is the estimated total for level
is the estimated total for level  , and
, and 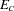 is the expected total for level
is the expected total for level  under the null hypothesis. For the null hypothesis of equal proportions, the expected total for each level equals
under the null hypothesis. For the null hypothesis of equal proportions, the expected total for each level equals
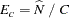 |
For specified null proportions, the expected total for level  equals
equals
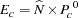 |
where 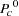 is the null proportion for level
is the null proportion for level  .
.
Under the null hypothesis of no association, the Rao-Scott likelihood ratio chi-square 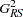 approximately follows a chi-square distribution with
approximately follows a chi-square distribution with 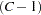 degrees of freedom. A better approximation can be obtained by the
degrees of freedom. A better approximation can be obtained by the 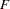 statistic,
statistic,
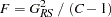 |
which has an 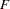 distribution with
distribution with 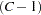 and
and 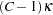 degrees of freedom under the null hypothesis, The value
degrees of freedom under the null hypothesis, The value  is the degrees of freedom for the variance estimator and depends on the sample design and the variance estimation method. The section Degrees of Freedom describes the computation of
is the degrees of freedom for the variance estimator and depends on the sample design and the variance estimation method. The section Degrees of Freedom describes the computation of  .
.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.