| The SEQDESIGN Procedure |
Example 77.7 Creating Whitehead’s Triangular Designs
This example requests three 4-stage Whitehead’s triangular designs for normally distributed statistics. Each design has a one-sided alternative hypothesis with early stopping to reject or accept the null hypothesis 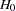 . Note that Whitehead’s triangular designs are different from unified family triangular designs.
. Note that Whitehead’s triangular designs are different from unified family triangular designs.
Suppose that a clinic is conducting a study of the effect of a new cancer treatment. The study consists of exposing mice to a carcinogen and randomly assigning them to either the control group or the treatment group. The event of interest is death from cancer induced by the carcinogen, and the response is the time from randomization to death.
Following the derivations in the section Test for Two Survival Distributions with a Log-Rank Test, the hypothesis 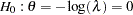 with an alternative hypothesis
with an alternative hypothesis 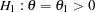 is used, where
is used, where 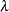 is the hazard ratio between the treatment group and the control group.
is the hazard ratio between the treatment group and the control group.
Also suppose that from past experience, the median survival time for the control group is  days, and the study wants to detect a
days, and the study wants to detect a 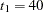 days’ median survival time with a
days’ median survival time with a 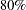 power in the trial. Assuming exponential survival functions for the two groups, the hazard rates can be computed from
power in the trial. Assuming exponential survival functions for the two groups, the hazard rates can be computed from
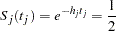 |
where 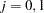 .
.
Thus, with 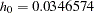 and
and  , the hazard ratio
, the hazard ratio 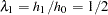 , and the alternative reference is
, and the alternative reference is
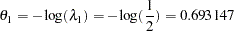 |
The following statements invoke the SEQDESIGN procedure and specify three Whitehead’s triangular designs:
ods graphics on;
proc seqdesign altref=0.693147
bscale=score
plots=combinedboundary
;
BoundaryKeyNone: design nstages=4
method=whitehead
boundarykey=none
alt=upper stop=both
alpha=0.05 beta=0.20
;
BoundaryKeyAlpha: design nstages=4
method=whitehead
boundarykey=alpha
alt=upper stop=both
alpha=0.05 beta=0.20
;
BoundaryKeyBeta: design nstages=4
method=whitehead
boundarykey=beta
alt=upper stop=both
alpha=0.05 beta=0.20
;
run;
ods graphics off;
Whitehead methods with early stopping to reject or accept the null hypothesis create boundaries that approximately satisfy the Type I and Type II error probability specification. The BOUNDARYKEY=NONE option specifies no adjustment to the boundary value at the final stage to maintain either a Type I or a Type II error probability level.
The "Design Information" table in Output 77.7.1 displays design specifications and maximum information. Note that with the BOUNDARYKEY=NONE option, the derived errors 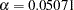 and
and 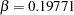 are not the same as the specified errors
are not the same as the specified errors 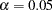 and
and 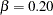 .
.
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Score |
| Alternative Hypothesis | Upper |
| Early Stop | Accept/Reject Null |
| Method | Whitehead |
| Boundary Key | None |
| Alternative Reference | 0.693147 |
| Number of Stages | 4 |
| Alpha | 0.05071 |
| Beta | 0.19771 |
| Power | 0.80229 |
| Max Information (Percent of Fixed Sample) | 129.6815 |
| Max Information | 16.70639 |
| Null Ref ASN (Percent of Fixed Sample) | 62.48184 |
| Alt Ref ASN (Percent of Fixed Sample) | 73.82535 |
The "Method Information" table in Output 77.7.2 displays the derived  and
and 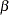 errors and the derived drift parameter. The derived errors
errors and the derived drift parameter. The derived errors 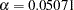 and
and 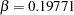 are not exactly the same as the specified errors
are not exactly the same as the specified errors 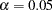 and
and 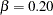 with the BOUNDARYKEY=NONE option.
with the BOUNDARYKEY=NONE option.
The "Boundary Information" table in Output 77.7.3 displays information level, alternative reference, and boundary values. With the specified BOUNDARYSCALE=SCORE option, the alternative reference and boundary values are displayed with the score statistics scale.
| Boundary Information (Score Scale) Null Reference = 0 |
|||||
|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | |||
| Information Level | Reference | Upper | |||
| Proportion | Actual | Upper | Beta | Alpha | |
| 1 | 0.2500 | 4.176597 | 2.89500 | -0.95755 | 4.78775 |
| 2 | 0.5000 | 8.353195 | 5.78999 | 1.91510 | 5.74530 |
| 3 | 0.7500 | 12.52979 | 8.68499 | 4.78775 | 6.70285 |
| 4 | 1.0000 | 16.70639 | 11.57998 | 7.66039 | 7.66039 |
With the specified ODS GRAPHICS ON statement, a detailed boundary plot with the rejection and acceptance regions is displayed by default, as shown in Output 77.7.4.
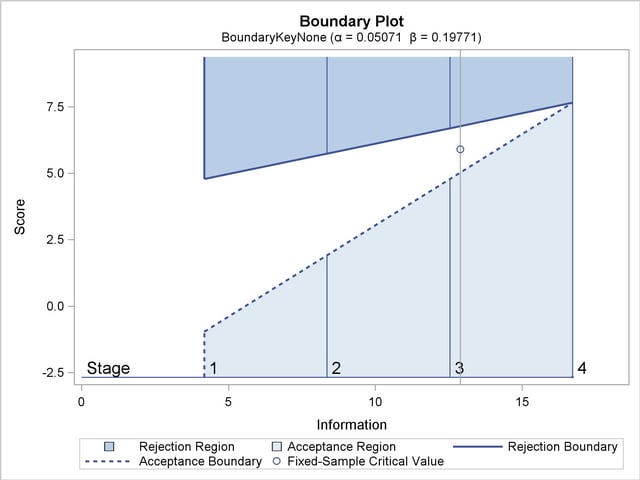
The second design uses the BOUNDARYKEY=ALPHA option to adjust the boundary value at the final stage to maintain the Type I error probability level.
The "Design Information" table in Output 77.7.5 displays design specifications and the derived maximum information. Note that with the BOUNDARYKEY=ALPHA option, the specified Type I error probability 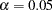 is maintained.
is maintained.
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Score |
| Alternative Hypothesis | Upper |
| Early Stop | Accept/Reject Null |
| Method | Whitehead |
| Boundary Key | Alpha |
| Alternative Reference | 0.693147 |
| Number of Stages | 4 |
| Alpha | 0.05 |
| Beta | 0.20044 |
| Power | 0.79956 |
| Max Information (Percent of Fixed Sample) | 129.9894 |
| Max Information | 16.70639 |
| Null Ref ASN (Percent of Fixed Sample) | 62.6302 |
| Alt Ref ASN (Percent of Fixed Sample) | 74.00064 |
The "Method Information" table in Output 77.7.6 displays the specified and derived  and
and 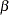 errors and the derived drift parameter. The derived Type I error probability is the same as the specified
errors and the derived drift parameter. The derived Type I error probability is the same as the specified 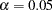 and the derived Type II error probability
and the derived Type II error probability 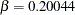 is not the same as the specified
is not the same as the specified 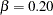 with the BOUNDARYKEY=ALPHA option.
with the BOUNDARYKEY=ALPHA option.
The "Boundary Information" table in Output 77.7.7 displays information level, alternative reference, and boundary values.
| Boundary Information (Score Scale) Null Reference = 0 |
|||||
|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | |||
| Information Level | Reference | Upper | |||
| Proportion | Actual | Upper | Beta | Alpha | |
| 1 | 0.2500 | 4.176597 | 2.89500 | -0.95755 | 4.78775 |
| 2 | 0.5000 | 8.353195 | 5.78999 | 1.91510 | 5.74530 |
| 3 | 0.7500 | 12.52979 | 8.68499 | 4.78775 | 6.70285 |
| 4 | 1.0000 | 16.70639 | 11.57998 | 7.81300 | 7.81300 |
With the specified ODS GRAPHICS ON statement, a detailed boundary plot with the rejection and acceptance regions is displayed by default, as shown in Output 77.7.8.
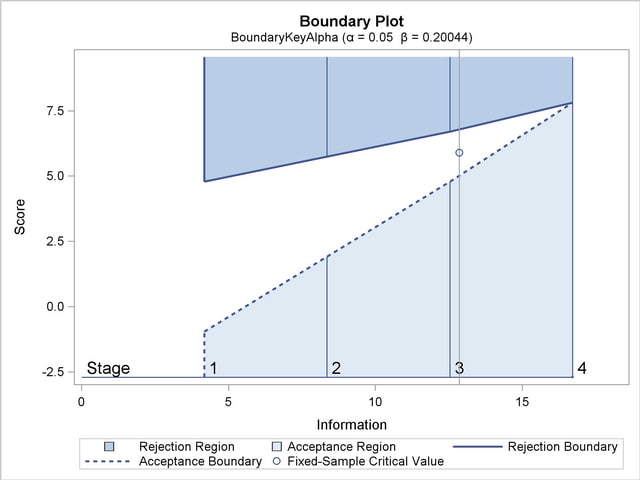
The third design specifies the BOUNDARYKEY=BETA option to derive the boundary values to maintain the Type II error probability level 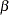 .
.
The "Design Information" table in Output 77.7.9 displays design specifications and the derived maximum information. Note that with the BOUNDARYKEY=BETA option, the specified Type II error probability 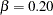 is maintained.
is maintained.
| Design Information | |
|---|---|
| Statistic Distribution | Normal |
| Boundary Scale | Score |
| Alternative Hypothesis | Upper |
| Early Stop | Accept/Reject Null |
| Method | Whitehead |
| Boundary Key | Beta |
| Alternative Reference | 0.693147 |
| Number of Stages | 4 |
| Alpha | 0.05011 |
| Beta | 0.2 |
| Power | 0.8 |
| Max Information (Percent of Fixed Sample) | 129.9364 |
| Max Information | 16.70639 |
| Null Ref ASN (Percent of Fixed Sample) | 62.60462 |
| Alt Ref ASN (Percent of Fixed Sample) | 73.97042 |
The "Method Information" table in Output 77.7.10 displays the  and
and 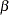 errors and the derived drift parameter. The derived Type II error probability is the same as the specified
errors and the derived drift parameter. The derived Type II error probability is the same as the specified 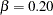 and the derived Type I error probability
and the derived Type I error probability 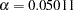 is not the same as the specified
is not the same as the specified 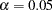 with the BOUNDARYKEY=BETA option.
with the BOUNDARYKEY=BETA option.
The "Boundary Information" table in Output 77.7.11 displays information level, alternative reference, and boundary values.
| Boundary Information (Score Scale) Null Reference = 0 |
|||||
|---|---|---|---|---|---|
| _Stage_ | Alternative | Boundary Values | |||
| Information Level | Reference | Upper | |||
| Proportion | Actual | Upper | Beta | Alpha | |
| 1 | 0.2500 | 4.176597 | 2.89500 | -0.95755 | 4.78775 |
| 2 | 0.5000 | 8.353195 | 5.78999 | 1.91510 | 5.74530 |
| 3 | 0.7500 | 12.52979 | 8.68499 | 4.78775 | 6.70285 |
| 4 | 1.0000 | 16.70639 | 11.57998 | 7.78899 | 7.78899 |
With the specified ODS GRAPHICS ON statement, a detailed boundary plot with the rejection and acceptance regions is displayed by default, as shown in Output 77.7.12.
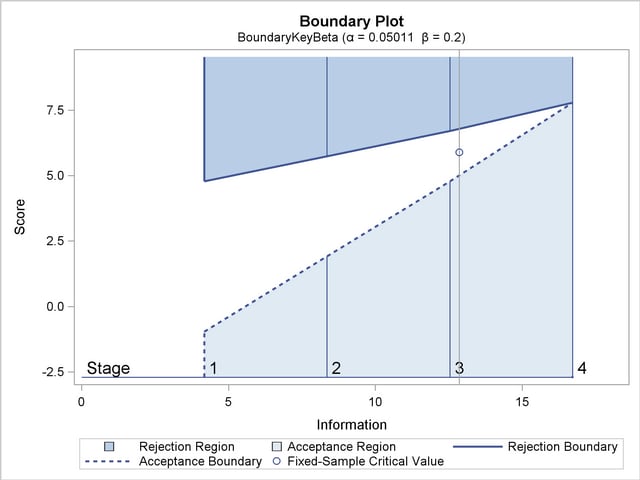
With the PLOTS=COMBINEDBOUNDARY option, a combined plot of group sequential boundaries for all designs is displayed, as shown in Output 77.7.13. It shows that three designs are similar, with a slightly smaller boundary value at the final stage for the design with the BOUNDARYKEY=NONE option.
The following statements invoke the SEQDESIGN procedure and specify the SAMPLESIZE statement to derive required sample sizes for a log-rank test comparing two survival distributions for the treatment effect (Jennison and Turnbull 2000 pp. 77–79; Whitehead 1997, pp. 36–39):
proc seqdesign altref=0.693147
bscale=score
;
BoundaryKeyAlpha: design nstages=4
method=whitehead
boundarykey=alpha
alt=upper stop=both
alpha=0.05 beta=0.20
;
samplesize model=twosamplesurvival
( nullhazard=0.03466 accrate=10);
run;
The design is identical to the previous design with the BOUNDARYKEY=ALPHA option except with the addition of the sample size computation.
The "Sample Size Summary" table in Output 77.7.14 displays parameters for the sample size computation. Since the ACCTIME= option is not specified for the accrual time, the minimum and maximum accrual times are derived for the specified accrual rate.
| Sample Size Summary | |
|---|---|
| Test | Two-Sample Survival |
| Null Hazard Rate | 0.03466 |
| Hazard Rate (Group A) | 0.01733 |
| Hazard Rate (Group B) | 0.03466 |
| Hazard Ratio | 0.5 |
| log(Hazard Ratio) | -0.69315 |
| Reference Hazards | Alt Ref |
| Accrual Rate | 10 |
| Min Accrual Time | 6.682556 |
| Min Sample Size | 66.82556 |
| Max Accrual Time | 25.40111 |
| Max Sample Size | 254.0111 |
| Max Number of Events | 66.82556 |
If the ACCTIME=20 option is specified in the SAMPLESIZE statement, the "Sample Size Summary" table in Output 77.7.15 also displays the follow-up time and maximum sample size with the specified accrual time.
| Sample Size Summary | |
|---|---|
| Test | Two-Sample Survival |
| Null Hazard Rate | 0.03466 |
| Hazard Rate (Group A) | 0.01733 |
| Hazard Rate (Group B) | 0.03466 |
| Hazard Ratio | 0.5 |
| log(Hazard Ratio) | -0.69315 |
| Reference Hazards | Alt Ref |
| Accrual Rate | 10 |
| Accrual Time | 20 |
| Follow-up Time | 6.474376 |
| Total Time | 26.47438 |
| Max Number of Events | 66.82556 |
| Max Sample Size | 200 |
| Expected Sample Size (Null Ref) | 161.5941 |
| Expected Sample Size (Alt Ref) | 172.4693 |
The "Number of Events (D) and Sample Sizes (N)" table in Output 77.7.16 displays the required time at each stage, in both fractional and integer numbers. The derived times under the heading "Fractional Time" are not integers. These times are rounded up to integers under the heading "Ceiling Time." The table also displays the numbers of events and sample sizes at each stage.
| Numbers of Events (D) and Sample Sizes (N) Two-Sample Log-Rank Test |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| _Stage_ | Fractional Time | Ceiling Time | ||||||||||||||
| D | D(Grp 1) | D(Grp 2) | Time | N | N(Grp 1) | N(Grp 2) | Information | D | D(Grp 1) | D(Grp 2) | Time | N | N(Grp 1) | N(Grp 2) | Information | |
| 1 | 16.71 | 5.82 | 10.89 | 11.9867 | 119.87 | 59.93 | 59.93 | 4.1766 | 16.74 | 5.83 | 10.91 | 12 | 120.00 | 60.00 | 60.00 | 4.1854 |
| 2 | 33.41 | 11.84 | 21.57 | 17.3585 | 173.58 | 86.79 | 86.79 | 8.3532 | 35.73 | 12.68 | 23.04 | 18 | 180.00 | 90.00 | 90.00 | 8.9322 |
| 3 | 50.12 | 18.01 | 32.11 | 21.7480 | 200.00 | 100.00 | 100.00 | 12.5298 | 51.07 | 18.37 | 32.70 | 22 | 200.00 | 100.00 | 100.00 | 12.7667 |
| 4 | 66.83 | 24.46 | 42.37 | 26.4744 | 200.00 | 100.00 | 100.00 | 16.7064 | 68.55 | 25.14 | 43.41 | 27 | 200.00 | 100.00 | 100.00 | 17.1378 |
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.