 |
 |
Example 74.1 Comparison of Robust Estimates
This example contrasts several of the robust methods available in the ROBUSTREG procedure.
The following statements generate 1000 random observations. The first 900 observations are from a linear model, and the last 100 observations are significantly biased in the  -direction. In other words, 10% of the observations are contaminated with outliers.
-direction. In other words, 10% of the observations are contaminated with outliers.
data a (drop=i);
do i=1 to 1000;
x1=rannor(1234);
x2=rannor(1234);
e=rannor(1234);
if i > 900 then y=100 + e;
else y=10 + 5*x1 + 3*x2 + .5 * e;
output;
end;
run;
The following statements invoke PROC REG and PROC ROBUSTREG with the data set a.
proc reg data=a;
model y = x1 x2;
run;
proc robustreg data=a method=m ;
model y = x1 x2;
run;
proc robustreg data=a method=mm;
model y = x1 x2;
run;
proc robustreg data=a method=s ;
model y = x1 x2;
run;
proc robustreg data=a method=lts ;
model y = x1 x2;
run;
The tables of parameter estimates generated with the ROBUSTREG procedure by using M estimation, MM estimation, S estimation, and LTS estimation are shown in Output 74.1.2, Output 74.1.3, Output 74.1.4, and Output 74.1.5, respectively. For comparison, the ordinary least squares (OLS) estimates produced by the REG procedure (
Chapter 73,
The REG Procedure
) are shown in Output 74.1.1. The four robust methods, M, MM, S, and LTS, correctly estimate the regression coefficients for the underlying model (10, 5, and 3), but the OLS estimate does not.
Output 74.1.1
OLS Estimates for Data with 10% Contamination
The REG Procedure
Model: MODEL1
Dependent Variable: y
| 1 |
19.06712 |
0.86322 |
22.09 |
<.0001 |
| 1 |
3.55485 |
0.86892 |
4.09 |
<.0001 |
| 1 |
2.12341 |
0.83039 |
2.56 |
0.0107 |
Output 74.1.2
M Estimates for Data with 10% Contamination
| WORK.A |
| y |
| 2 |
| 1000 |
| M Estimation |
| 1 |
10.0024 |
0.0174 |
9.9683 |
10.0364 |
331908 |
<.0001 |
| 1 |
5.0077 |
0.0175 |
4.9735 |
5.0420 |
82106.9 |
<.0001 |
| 1 |
3.0161 |
0.0167 |
2.9834 |
3.0488 |
32612.5 |
<.0001 |
| 1 |
0.5780 |
|
|
|
|
|
Output 74.1.3
MM Estimates for Data with 10% Contamination
| WORK.A |
| y |
| 2 |
| 1000 |
| MM Estimation |
| 1 |
10.0035 |
0.0176 |
9.9690 |
10.0379 |
323947 |
<.0001 |
| 1 |
5.0085 |
0.0178 |
4.9737 |
5.0433 |
79600.6 |
<.0001 |
| 1 |
3.0181 |
0.0168 |
2.9851 |
3.0511 |
32165.0 |
<.0001 |
| 0 |
0.6733 |
|
|
|
|
|
Output 74.1.4
S Estimates for Data with 10% Contamination
| WORK.A |
| y |
| 2 |
| 1000 |
| S Estimation |
| 1 |
10.0055 |
0.0180 |
9.9703 |
10.0408 |
309917 |
<.0001 |
| 1 |
5.0096 |
0.0182 |
4.9740 |
5.0452 |
76045.2 |
<.0001 |
| 1 |
3.0210 |
0.0172 |
2.9873 |
3.0547 |
30841.3 |
<.0001 |
| 0 |
0.6721 |
|
|
|
|
|
Output 74.1.5
LTS Estimates for Data with 10% Contamination
| WORK.A |
| y |
| 2 |
| 1000 |
| LTS Estimation |
| 1 |
10.0083 |
| 1 |
5.0316 |
| 1 |
3.0396 |
| 0 |
0.5880 |
| 0 |
0.5113 |
The next statements demonstrate that if the percentage of contamination is increased to  , the M method and the MM method with default options fail to estimate the underlying model. Output 74.1.6 and Output 74.1.7 display these estimates. However, by tuning the constant
, the M method and the MM method with default options fail to estimate the underlying model. Output 74.1.6 and Output 74.1.7 display these estimates. However, by tuning the constant  for the M method and the constants INITH and K0 for the MM method, you can increase the breakdown values of the estimates and capture the right model. Output 74.1.8 and Output 74.1.9 display these estimates. Similarly, you can tune the constant EFF for the S method and the constant H for the LTS method and correctly estimate the underlying model with these methods. Results are not presented.
for the M method and the constants INITH and K0 for the MM method, you can increase the breakdown values of the estimates and capture the right model. Output 74.1.8 and Output 74.1.9 display these estimates. Similarly, you can tune the constant EFF for the S method and the constant H for the LTS method and correctly estimate the underlying model with these methods. Results are not presented.
data b (drop=i);
do i=1 to 1000;
x1=rannor(1234);
x2=rannor(1234);
e=rannor(1234);
if i > 600 then y=100 + e;
else y=10 + 5*x1 + 3*x2 + .5 * e;
output;
end;
run;
proc robustreg data=b method=m ;
model y = x1 x2;
run;
proc robustreg data=b method=mm;
model y = x1 x2;
run;
proc robustreg data=b method=m(wf=bisquare(c=2));
model y = x1 x2;
run;
proc robustreg data=b method=mm(inith=502 k0=1.8);
model y = x1 x2;
run;
Output 74.1.6
M Estimates (Default Setting) for Data with 40% Contamination
| WORK.B |
| y |
| 2 |
| 1000 |
| M Estimation |
| 1 |
44.8991 |
1.5609 |
41.8399 |
47.9584 |
827.46 |
<.0001 |
| 1 |
2.4309 |
1.5712 |
-0.6485 |
5.5104 |
2.39 |
0.1218 |
| 1 |
1.3742 |
1.5015 |
-1.5687 |
4.3171 |
0.84 |
0.3601 |
| 1 |
56.6342 |
|
|
|
|
|
Output 74.1.7
MM Estimates (Default Setting) for Data with 40% Contamination
| WORK.B |
| y |
| 2 |
| 1000 |
| MM Estimation |
| 1 |
43.0607 |
1.7978 |
39.5370 |
46.5844 |
573.67 |
<.0001 |
| 1 |
2.7369 |
1.8140 |
-0.8185 |
6.2924 |
2.28 |
0.1314 |
| 1 |
1.5211 |
1.7265 |
-1.8628 |
4.9049 |
0.78 |
0.3783 |
| 0 |
52.8496 |
|
|
|
|
|
Output 74.1.8
M Estimates (Tuned) for Data with 40% Contamination
| WORK.B |
| y |
| 2 |
| 1000 |
| M Estimation |
| 1 |
10.0137 |
0.0219 |
9.9708 |
10.0565 |
209688 |
<.0001 |
| 1 |
4.9905 |
0.0220 |
4.9473 |
5.0336 |
51399.1 |
<.0001 |
| 1 |
3.0399 |
0.0210 |
2.9987 |
3.0811 |
20882.4 |
<.0001 |
| 1 |
1.0531 |
|
|
|
|
|
Output 74.1.9
MM Estimates (Tuned) for Data with 40% Contamination
| WORK.B |
| y |
| 2 |
| 1000 |
| MM Estimation |
| 1 |
10.0103 |
0.0213 |
9.9686 |
10.0520 |
221639 |
<.0001 |
| 1 |
4.9890 |
0.0218 |
4.9463 |
5.0316 |
52535.9 |
<.0001 |
| 1 |
3.0363 |
0.0201 |
2.9970 |
3.0756 |
22895.5 |
<.0001 |
| 0 |
1.8992 |
|
|
|
|
|
When there are bad leverage points, the M method fails to estimate the underlying model no matter what constant  you use. In this case, other methods (LTS, S, and MM) in PROC ROBUSTREG, which are robust to bad leverage points, will correctly estimate the underlying model.
you use. In this case, other methods (LTS, S, and MM) in PROC ROBUSTREG, which are robust to bad leverage points, will correctly estimate the underlying model.
The following statements generate 1000 observations with 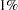 bad high leverage points.
bad high leverage points.
data c (drop=i);
do i=1 to 1000;
x1=rannor(1234);
x2=rannor(1234);
e=rannor(1234);
if i > 600 then y=100 + e;
else y=10 + 5*x1 + 3*x2 + .5 * e;
if i < 11 then x1=200 * rannor(1234);
if i < 11 then x2=200 * rannor(1234);
if i < 11 then y= 100*e;
output;
end;
run;
proc robustreg data=c method=mm(inith=502 k0=1.8);
model y = x1 x2;
run;
proc robustreg data=c method=s(k0=1.8);
model y = x1 x2;
run;
proc robustreg data=c method=lts(h=502);
model y = x1 x2;
run;
Output 74.1.10 displays the MM estimates with initial LTS estimates, Output 74.1.11 displays the S estimates, and Output 74.1.12 displays the LTS estimates.
Output 74.1.10
MM Estimates for Data with 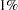 Leverage Points
Leverage Points
| WORK.C |
| y |
| 2 |
| 1000 |
| MM Estimation |
| 1 |
9.9820 |
0.0215 |
9.9398 |
10.0241 |
215369 |
<.0001 |
| 1 |
5.0303 |
0.0206 |
4.9898 |
5.0707 |
59469.1 |
<.0001 |
| 1 |
3.0222 |
0.0221 |
2.9789 |
3.0655 |
18744.9 |
<.0001 |
| 0 |
2.2134 |
|
|
|
|
|
Output 74.1.11
S Estimates for Data with 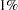 Leverage Points
Leverage Points
| WORK.C |
| y |
| 2 |
| 1000 |
| S Estimation |
| 1 |
9.9808 |
0.0216 |
9.9383 |
10.0232 |
212532 |
<.0001 |
| 1 |
5.0303 |
0.0208 |
4.9896 |
5.0710 |
58656.3 |
<.0001 |
| 1 |
3.0217 |
0.0222 |
2.9782 |
3.0652 |
18555.7 |
<.0001 |
| 0 |
2.2094 |
|
|
|
|
|
Output 74.1.12
LTS Estimates for Data with 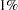 Leverage Points
Leverage Points
| WORK.C |
| y |
| 2 |
| 1000 |
| LTS Estimation |
| 1 |
9.9742 |
| 1 |
5.0010 |
| 1 |
3.0219 |
| 0 |
0.9952 |
| 0 |
0.5216 |
Copyright
© 2009 by SAS Institute Inc., Cary, NC, USA. All
rights reserved.
 -direction. In other words, 10% of the observations are contaminated with outliers.
-direction. In other words, 10% of the observations are contaminated with outliers.  , the M method and the MM method with default options fail to estimate the underlying model. Output 74.1.6 and Output 74.1.7 display these estimates. However, by tuning the constant
, the M method and the MM method with default options fail to estimate the underlying model. Output 74.1.6 and Output 74.1.7 display these estimates. However, by tuning the constant  for the M method and the constants INITH and K0 for the MM method, you can increase the breakdown values of the estimates and capture the right model. Output 74.1.8 and Output 74.1.9 display these estimates. Similarly, you can tune the constant EFF for the S method and the constant H for the LTS method and correctly estimate the underlying model with these methods. Results are not presented.
for the M method and the constants INITH and K0 for the MM method, you can increase the breakdown values of the estimates and capture the right model. Output 74.1.8 and Output 74.1.9 display these estimates. Similarly, you can tune the constant EFF for the S method and the constant H for the LTS method and correctly estimate the underlying model with these methods. Results are not presented.  you use. In this case, other methods (LTS, S, and MM) in PROC ROBUSTREG, which are robust to bad leverage points, will correctly estimate the underlying model.
you use. In this case, other methods (LTS, S, and MM) in PROC ROBUSTREG, which are robust to bad leverage points, will correctly estimate the underlying model. 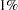 bad high leverage points.
bad high leverage points.