Fit Plot

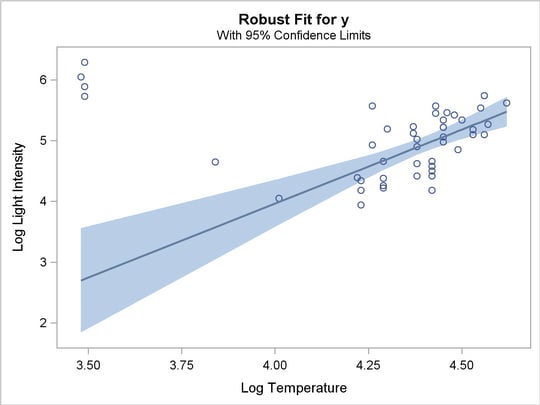
When the model has a single independent continuous variable (with or without the intercept), the ROBUSTREG procedure automatically creates a plot of robust fit against this independent variable.

The following simple example is used to show the fit plot. The data, from Rousseeuw and Leroy (1987, Table 3), include the logarithm of surface temperature and the logarithm of light intensity for 47 stars in the direction of the constellation Cygnus.

   data star;
      input index x y @@;
      label x = 'Log Temperature'
            y = 'Log Light Intensity';
   datalines;
   1   4.37  5.23     25  4.38  5.02
   2   4.56  5.74     26  4.42  4.66
   3   4.26  4.93     27  4.29  4.66
   4   4.56  5.74     28  4.38  4.90
   5   4.30  5.19     29  4.22  4.39
   6   4.46  5.46     30  3.48  6.05
   7   3.84  4.65     31  4.38  4.42
   8   4.57  5.27     32  4.56  5.10
   9   4.26  5.57     33  4.45  5.22
   10  4.37  5.12     34  3.49  6.29
   11  3.49  5.73     35  4.23  4.34
   12  4.43  5.45     36  4.62  5.62
   13  4.48  5.42     37  4.53  5.10
   14  4.01  4.05     38  4.45  5.22
   15  4.29  4.26     39  4.53  5.18
   16  4.42  4.58     40  4.43  5.57
   17  4.23  3.94     41  4.38  4.62
   18  4.42  4.18     42  4.45  5.06
   19  4.23  4.18     43  4.50  5.34
   20  3.49  5.89     44  4.45  5.34
   21  4.29  4.38     45  4.55  5.54
   22  4.29  4.22     46  4.45  4.98
   23  4.42  4.42     47  4.42  4.50
   24  4.49  4.85
   ;

The fit plot in Figure 74.17, created with the following statements, plots the robust fit of the logarithm of light intensity with the MM method against the logarithm of the surface temperature.

   ods graphics on;
    
   proc robustreg data=star method=mm ;
       model y = x;
   run;
    
   ods graphics off;

Confidence limits are added on the plot by default. The NOLIMITS option suppresses these limits.

Figure 74.17 Robust Fit

   ods graphics on;
    
   proc robustreg data=star method=mm plot=fitplot(nolimits);
       model y = x;
   run;
    
   ods graphics off;

Distance-Distance Plot

The distance-distance plot (DDPLOT) is mainly used for leverage-point diagnostics. It is a scatter plot of the robust distances against the classical Mahalanobis distances for the continuous independent variables. See the section Leverage Point and Outlier Detection for details about the robust distance. If there is a classification variable specified in the model, this plot is not created.

You can use the PLOT=DDPLOT option to request this plot. The following statements use the stack data set in the section M Estimation to create the single plot shown in Figure 74.5.

   ods graphics on;
    
   proc robustreg data=stack plot=ddplot;
      model y = x1 x2 x3;
   run;
    
   ods graphics off;

The reference lines represent the cutoff values. The diagonal line is also drawn to show the distribution of the distances. By default, all outliers and leverage points are labeled with observation numbers. To change the default, you can use the LABEL= option as described in Table 74.2.

If you specify ID variables in the ID statement, instead of observation numbers, the values of the first ID variable are used as labels.

Residual-Distance Plot

The residual-distance plot (RDPLOT) is used for both outlier and leverage-point diagnostics. It is a scatter plot of the standardized robust residuals against the robust distances. See the section Leverage Point and Outlier Detection for details about the robust distance. If there is a classification variable specified in the model, this plot is not created.

You can use the PLOT=RDPLOT option to request this plot. The following statements use the stack data set in the section M Estimation to create a single plot shown in Figure 74.4.

   ods graphics on;
    
   proc robustreg data=stack plot=rdplot;
      model y = x1 x2 x3;
   run;
    
   ods graphics off;

The reference lines represent the cutoff values. By default, all outliers and leverage points are labeled with observation numbers. To change the default, you can use the LABEL= option as described in Table 74.2.

If you specify ID variables in the ID statement instead of observation numbers, the values of the first ID variable are used as labels.

Histogram and Q-Q Plot

PROC ROBUSTREG produces a histogram and a Q-Q plot for the standardized robust residuals. The histogram is superimposed with a normal density curve and a kernel density curve. Using the stack data set in the section M Estimation, the following statements create the plots in Figure 74.6 and Figure 74.7.

   ods graphics on;
    
   proc robustreg data=stack plots=(histogram qqplot);
      model y = x1 x2 x3;
   run;
    
   ods graphics off;

ODS Graph Names

PROC ROBUSTREG assigns a name to each graph it creates using ODS. You can use these names to reference the graphs when using ODS. The names are listed in Table 74.11.

To request these graphs you must specify the ODS GRAPHICS statement in addition to the PLOTS= option described in Table 74.10. For more information about the ODS GRAPHICS statement, see Chapter 21, Statistical Graphics Using ODS.