| The PRINCOMP Procedure |
Example 69.1 Temperatures
This example analyzes mean daily temperatures in selected cities in January and July. Both the raw data and the principal components are plotted to illustrate how principal components are orthogonal rotations of the original variables.
The following statements create the Temperature data set.
data Temperature;
length Cityid $ 2;
title 'Mean Temperature in January and July for Selected Cities ';
input City $1-15 January July;
Cityid = substr(City,1,2);
datalines;
Mobile 51.2 81.6
Phoenix 51.2 91.2
Little Rock 39.5 81.4
Sacramento 45.1 75.2
Denver 29.9 73.0
Hartford 24.8 72.7
Wilmington 32.0 75.8
Washington DC 35.6 78.7
Jacksonville 54.6 81.0
Miami 67.2 82.3
Atlanta 42.4 78.0
Boise 29.0 74.5
Chicago 22.9 71.9
Peoria 23.8 75.1
Indianapolis 27.9 75.0
Des Moines 19.4 75.1
Wichita 31.3 80.7
Louisville 33.3 76.9
New Orleans 52.9 81.9
Portland, ME 21.5 68.0
Baltimore 33.4 76.6
Boston 29.2 73.3
Detroit 25.5 73.3
Sault Ste Marie 14.2 63.8
Duluth 8.5 65.6
Minneapolis 12.2 71.9
Jackson 47.1 81.7
Kansas City 27.8 78.8
St Louis 31.3 78.6
Great Falls 20.5 69.3
Omaha 22.6 77.2
Reno 31.9 69.3
Concord 20.6 69.7
Atlantic City 32.7 75.1
Albuquerque 35.2 78.7
Albany 21.5 72.0
Buffalo 23.7 70.1
New York 32.2 76.6
Charlotte 42.1 78.5
Raleigh 40.5 77.5
Bismarck 8.2 70.8
Cincinnati 31.1 75.6
Cleveland 26.9 71.4
Columbus 28.4 73.6
Oklahoma City 36.8 81.5
Portland, OR 38.1 67.1
Philadelphia 32.3 76.8
Pittsburgh 28.1 71.9
Providence 28.4 72.1
Columbia 45.4 81.2
Sioux Falls 14.2 73.3
Memphis 40.5 79.6
Nashville 38.3 79.6
Dallas 44.8 84.8
El Paso 43.6 82.3
Houston 52.1 83.3
Salt Lake City 28.0 76.7
Burlington 16.8 69.8
Norfolk 40.5 78.3
Richmond 37.5 77.9
Spokane 25.4 69.7
Charleston, WV 34.5 75.0
Milwaukee 19.4 69.9
Cheyenne 26.6 69.1
;
The following statements plot the temperature data set. The Cityid variable instead of City is used as a data label in the scatter plot for possible label clashing.
title 'Mean Temperature in January and July for Selected Cities';
title2 'Plot of Raw Data';
proc sgplot data=Temperature;
scatter x=July y=January / datalabel=Cityid;
run;
The results are displayed in Output 69.1.1, which shows a scatter diagram of the 64 pairs of data points with July temperatures plotted against January temperatures.
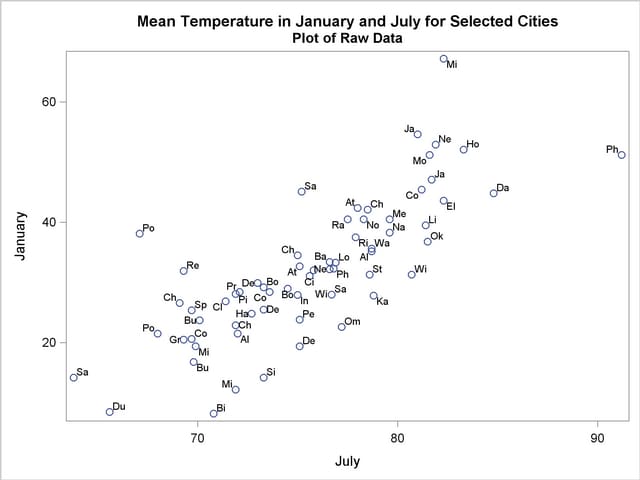
The following statement requests a principal component analysis on the Temperature data set:
ods graphics on;
title 'Mean Temperature in January and July for Selected Cities';
proc princomp data=Temperature cov plots=score(ellipse);
var July January;
id Cityid;
run;
ods graphics off;
Output 69.1.2 displays the PROC PRINCOMP output. The standard deviation of January (11.712) is higher than the standard deviation of July (5.128). The COV option in the PROC PRINCOMP statement requests the principal components to be computed from the covariance matrix. The total variance is 163.474. The first principal component explains about 94% of the total variance, and the second principal component explains only about 6%. The eigenvalues sum to the total variance.
Note that January receives a higher loading on Prin1 because it has a higher standard deviation than July, and the PRINCOMP procedure calculates the scores by using the centered variables rather than the standardized variables.
| Observations | 64 |
|---|---|
| Variables | 2 |
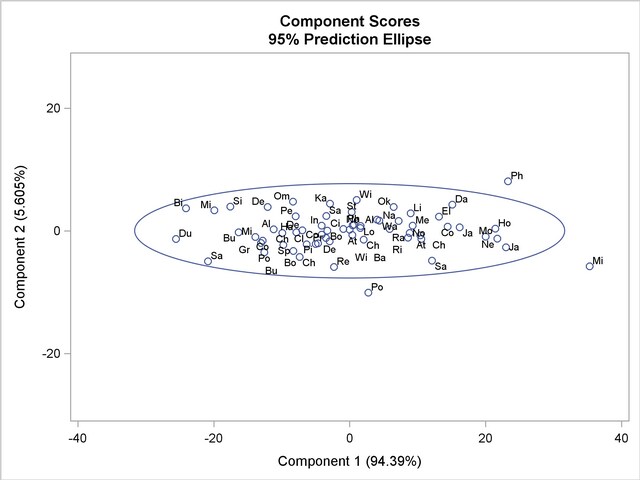
PLOTS=SCORE in the PROC PRINCOMP statement requests a plot of the second principal component against the first principal component as shown in Output 69.1.3. It is clear from this plot that the principal components are orthogonal rotations of the original variables and that the first principal component has a larger variance than the second principal component. In fact, the first component has a larger variance than either of the original variables July and January. The ellipse indicates that Miami, Phoenix, and Portland are possible outliers.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.