 |
|
| The PHREG Procedure |
Example 64.13 Bayesian Analysis of the Cox Model
This example illustrates the use of an informative prior. Hazard ratios, which are transformations of the regression parameters, are useful for interpreting survival models. This example also demonstrates the use of the HAZARDRATIO statement to obtain customized hazard ratios.
Consider the VALung data set in Example 64.3. In this example, the Cox model is used for the Bayesian analysis. The parameters are the coefficients of the continuous explanatory variables (Kps, Duration, and Age) and the coefficients of the design variables for the categorical explanatory variables (Prior, Cell, and Therapy). You use the CLASS statement in PROC PHREG to specify the categorical variables and their reference levels. Using the default reference parameterization, the design variables for the categorical variables are Prioryes (for Prior with Prior=’no’ as reference), Celladeno, Cellsmall, Cellsquamous (for Cell with Cell=’large’ as reference), and Therapytest (for Therapy=’standard’ as reference).
Consider the explanatory variable Kps. The Karnofsky performance scale index enables patients to be classified according to their functional impairment. The scale can range from 0 to 100—0 for dead, and 100 for a normal, healthy person with no evidence of disease. Recall that a flat prior was used for the regression coefficient in the example in the section Bayesian Analysis. A flat prior on the Kps coefficient implies that the coefficient is as likely to be 0.1 as it is to be –100000. A coefficient of –5 means that a decrease of 20 points in the scale increases the hazard by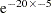 
(=2.68 
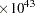)-fold, which is a rather unreasonable and unrealistic expectation for the effect of the Karnofsky index, much less than the value of –100000. Suppose you have a more realistic expectation: the effect is somewhat small and is more likely to be negative than positive, and a decrease of 20 points in the Karnofsky index will change the hazard from 0.9-fold (some minor positive effect) to 4-fold (a large negative effect). You can convert this opinion to a more informative prior on the Kps coefficient 
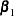. Mathematically,
 |
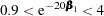which is equivalent to
 |
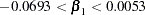This becomes the plausible range that you believe the Kps coefficient can take. Now you can find a normal distribution that best approximates this belief by placing the majority of the prior distribution mass within this range. Assuming this interval is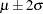 
, where 
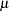and 
are the mean and standard deviation of the normal prior, respectively, the hyperparameters 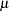and are computed as follows:
 |
 |
 |
|||
 |
|
 |
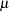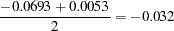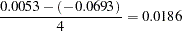Note that a normal prior distribution with mean –0.0320 and standard deviation 0.0186 indicates that you believe, before looking at the data, that a decrease of 20 points in the Karnofsky index will probably change the hazard rate by 0.9-fold to 4-fold. This does not rule out the possibility that the Kps coefficient can take a more extreme value such as –5, but the probability of having such extreme values is very small.
Assume the prior distributions are independent for all the parameters. For the coefficient of Kps, you use a normal prior distribution with mean –0.0320 and variance 
=0.00035). For other parameters, you resort to using a normal prior distribution with mean 0 and variance 
, which is fairly noninformative. Means and variances of these independent normal distributions are saved in the data set Prior as follows:
proc format;
value yesno 0='no' 10='yes';
run;
data VALung;
drop check m;
retain Therapy Cell;
infile cards column=column;
length Check $ 1;
label Time='time to death in days'
Kps='Karnofsky performance scale'
Duration='months from diagnosis to randomization'
Age='age in years'
Prior='prior therapy'
Cell='cell type'
Therapy='type of treatment';
format Prior yesno.;
M=Column;
input Check $ @@;
if M>Column then M=1;
if Check='s'|Check='t' then do;
input @M Therapy $ Cell $;
delete;
end;
else do;
input @M Time Kps Duration Age Prior @@;
Status=(Time>0);
Time=abs(Time);
end;
datalines;
standard squamous
72 60 7 69 0 411 70 5 64 10 228 60 3 38 0 126 60 9 63 10
118 70 11 65 10 10 20 5 49 0 82 40 10 69 10 110 80 29 68 0
314 50 18 43 0 -100 70 6 70 0 42 60 4 81 0 8 40 58 63 10
144 30 4 63 0 -25 80 9 52 10 11 70 11 48 10
standard small
30 60 3 61 0 384 60 9 42 0 4 40 2 35 0 54 80 4 63 10
13 60 4 56 0 -123 40 3 55 0 -97 60 5 67 0 153 60 14 63 10
59 30 2 65 0 117 80 3 46 0 16 30 4 53 10 151 50 12 69 0
22 60 4 68 0 56 80 12 43 10 21 40 2 55 10 18 20 15 42 0
139 80 2 64 0 20 30 5 65 0 31 75 3 65 0 52 70 2 55 0
287 60 25 66 10 18 30 4 60 0 51 60 1 67 0 122 80 28 53 0
27 60 8 62 0 54 70 1 67 0 7 50 7 72 0 63 50 11 48 0
392 40 4 68 0 10 40 23 67 10
standard adeno
8 20 19 61 10 92 70 10 60 0 35 40 6 62 0 117 80 2 38 0
132 80 5 50 0 12 50 4 63 10 162 80 5 64 0 3 30 3 43 0
95 80 4 34 0
standard large
177 50 16 66 10 162 80 5 62 0 216 50 15 52 0 553 70 2 47 0
278 60 12 63 0 12 40 12 68 10 260 80 5 45 0 200 80 12 41 10
156 70 2 66 0 -182 90 2 62 0 143 90 8 60 0 105 80 11 66 0
103 80 5 38 0 250 70 8 53 10 100 60 13 37 10
test squamous
999 90 12 54 10 112 80 6 60 0 -87 80 3 48 0 -231 50 8 52 10
242 50 1 70 0 991 70 7 50 10 111 70 3 62 0 1 20 21 65 10
587 60 3 58 0 389 90 2 62 0 33 30 6 64 0 25 20 36 63 0
357 70 13 58 0 467 90 2 64 0 201 80 28 52 10 1 50 7 35 0
30 70 11 63 0 44 60 13 70 10 283 90 2 51 0 15 50 13 40 10
test small
25 30 2 69 0 -103 70 22 36 10 21 20 4 71 0 13 30 2 62 0
87 60 2 60 0 2 40 36 44 10 20 30 9 54 10 7 20 11 66 0
24 60 8 49 0 99 70 3 72 0 8 80 2 68 0 99 85 4 62 0
61 70 2 71 0 25 70 2 70 0 95 70 1 61 0 80 50 17 71 0
51 30 87 59 10 29 40 8 67 0
test adeno
24 40 2 60 0 18 40 5 69 10 -83 99 3 57 0 31 80 3 39 0
51 60 5 62 0 90 60 22 50 10 52 60 3 43 0 73 60 3 70 0
8 50 5 66 0 36 70 8 61 0 48 10 4 81 0 7 40 4 58 0
140 70 3 63 0 186 90 3 60 0 84 80 4 62 10 19 50 10 42 0
45 40 3 69 0 80 40 4 63 0
test large
52 60 4 45 0 164 70 15 68 10 19 30 4 39 10 53 60 12 66 0
15 30 5 63 0 43 60 11 49 10 340 80 10 64 10 133 75 1 65 0
111 60 5 64 0 231 70 18 67 10 378 80 4 65 0 49 30 3 37 0
;
data Prior;
input _TYPE_ $ Kps Duration Age Prioryes Celladeno Cellsmall
Cellsquamous Therapytest;
datalines;
Mean -0.0320 0 0 0 0 0 0 0
Var 0.00035 1e6 1e6 1e6 1e6 1e6 1e6 1e6
;
run;
In the following BAYES statement, COEFFPRIOR=NORMAL(INPUT=Prior) specifies the normal prior distribution for the regression coefficients with details contained in the data set Prior. Summary statistics of the posterior distribution are produced by default. Autocorrelations and effective sample size are requested as convergence diagnostics as well as the trace plots for visual analysis. For comparisons of hazards, three HAZARDRATIO statements are specified—one for the variable Therapy, one for the variable Age, and one for the variable Cell.
ods graphics on;
proc phreg data=VALung;
class Prior(ref='no') Cell(ref='large') Therapy(ref='standard');
model Time*Status(0) = Kps Duration Age Prior Cell Therapy;
bayes seed=1 coeffprior=normal(input=Prior) diagnostic=(autocorr ess)
plots=trace;
hazardratio 'Hazard Ratio Statement 1' Therapy;
hazardratio 'Hazard Ratio Statement 2' Age / unit=10;
hazardratio 'Hazard Ratio Statement 3' Cell;
run;
ods graphics off;
This analysis generates a posterior chain of 10,000 iterations after 2,000 iterations of burn-in, as depicted in Output 64.13.1.
| Model Information | ||
|---|---|---|
| Data Set | WORK.VALUNG | |
| Dependent Variable | Time | time to death in days |
| Censoring Variable | Status | |
| Censoring Value(s) | 0 | |
| Model | Cox | |
| Ties Handling | BRESLOW | |
| Burn-In Size | 2000 | |
| MC Sample Size | 10000 | |
| Thinning | 1 | |
Output 64.13.2 displays the names of the parameters and their corresponding effects and categories.
PROC PHREG computes the maximum likelihood estimates of regression parameters (Output 64.13.3). These estimates are used as the starting values for the simulation of posterior samples.
| Maximum Likelihood Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error |
95% Confidence Limits | |
| Kps | 1 | -0.0326 | 0.00551 | -0.0434 | -0.0218 |
| Duration | 1 | -0.00009 | 0.00913 | -0.0180 | 0.0178 |
| Age | 1 | -0.00855 | 0.00930 | -0.0268 | 0.00969 |
| Prioryes | 1 | 0.0723 | 0.2321 | -0.3826 | 0.5273 |
| Celladeno | 1 | 0.7887 | 0.3027 | 0.1955 | 1.3819 |
| Cellsmall | 1 | 0.4569 | 0.2663 | -0.0650 | 0.9787 |
| Cellsquamous | 1 | -0.3996 | 0.2827 | -0.9536 | 0.1544 |
| Therapytest | 1 | 0.2899 | 0.2072 | -0.1162 | 0.6961 |
Output 64.13.4 displays the independent normal prior for the analysis.
Fit statistics are displayed in Output 64.13.5. These statistics are useful for variable selection.
Summary statistics of the posterior samples are shown in Output 64.13.6 and Output 64.13.7. These results are quite comparable to the classical results based on maximizing the likelihood as shown in Output 64.13.3, since the prior distribution for the regression coefficients is relatively flat.
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| Kps | 10000 | -0.0326 | 0.00523 | -0.0362 | -0.0326 | -0.0291 |
| Duration | 10000 | -0.00159 | 0.00954 | -0.00756 | -0.00093 | 0.00504 |
| Age | 10000 | -0.00844 | 0.00928 | -0.0147 | -0.00839 | -0.00220 |
| Prioryes | 10000 | 0.0742 | 0.2348 | -0.0812 | 0.0737 | 0.2337 |
| Celladeno | 10000 | 0.7881 | 0.3065 | 0.5839 | 0.7876 | 0.9933 |
| Cellsmall | 10000 | 0.4639 | 0.2709 | 0.2817 | 0.4581 | 0.6417 |
| Cellsquamous | 10000 | -0.4024 | 0.2862 | -0.5927 | -0.4025 | -0.2106 |
| Therapytest | 10000 | 0.2892 | 0.2038 | 0.1528 | 0.2893 | 0.4240 |
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| Kps | 0.050 | -0.0429 | -0.0222 | -0.0433 | -0.0226 |
| Duration | 0.050 | -0.0220 | 0.0156 | -0.0210 | 0.0164 |
| Age | 0.050 | -0.0263 | 0.00963 | -0.0265 | 0.00941 |
| Prioryes | 0.050 | -0.3936 | 0.5308 | -0.3832 | 0.5384 |
| Celladeno | 0.050 | 0.1879 | 1.3920 | 0.1764 | 1.3755 |
| Cellsmall | 0.050 | -0.0571 | 1.0167 | -0.0888 | 0.9806 |
| Cellsquamous | 0.050 | -0.9687 | 0.1635 | -0.9641 | 0.1667 |
| Therapytest | 0.050 | -0.1083 | 0.6930 | -0.1284 | 0.6710 |
With autocorrelations retreating quickly to 0 (Output 64.13.8) and large effective sample sizes (Output 64.13.9), both diagnostics indicate a reasonably good mixing of the Markov chain. The trace plots in Output 64.13.10 also confirm the convergence of the Markov chain.
| Posterior Autocorrelations | ||||
|---|---|---|---|---|
| Parameter | Lag 1 | Lag 5 | Lag 10 | Lag 50 |
| Kps | 0.1442 | -0.0016 | 0.0096 | -0.0013 |
| Duration | 0.2672 | -0.0054 | -0.0004 | -0.0011 |
| Age | 0.1374 | -0.0044 | 0.0129 | 0.0084 |
| Prioryes | 0.2507 | -0.0271 | -0.0012 | 0.0004 |
| Celladeno | 0.4160 | 0.0265 | -0.0062 | 0.0190 |
| Cellsmall | 0.5055 | 0.0277 | -0.0011 | 0.0271 |
| Cellsquamous | 0.3586 | 0.0252 | -0.0044 | 0.0107 |
| Therapytest | 0.2063 | 0.0199 | -0.0047 | -0.0166 |
| Effective Sample Sizes | |||
|---|---|---|---|
| Parameter | ESS | Correlation Time |
Efficiency |
| Kps | 7046.7 | 1.4191 | 0.7047 |
| Duration | 5790.0 | 1.7271 | 0.5790 |
| Age | 7426.1 | 1.3466 | 0.7426 |
| Prioryes | 6102.2 | 1.6388 | 0.6102 |
| Celladeno | 3673.4 | 2.7223 | 0.3673 |
| Cellsmall | 3346.4 | 2.9883 | 0.3346 |
| Cellsquamous | 4052.8 | 2.4674 | 0.4053 |
| Therapytest | 6870.8 | 1.4554 | 0.6871 |
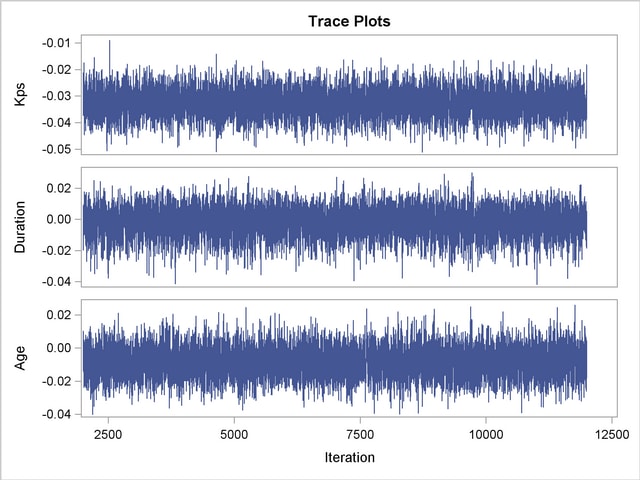
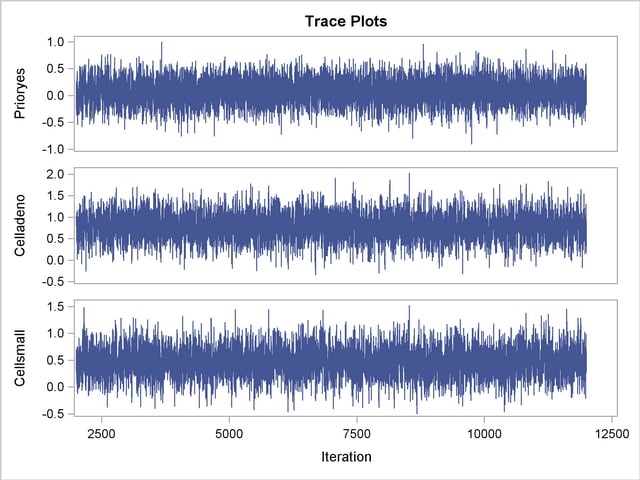
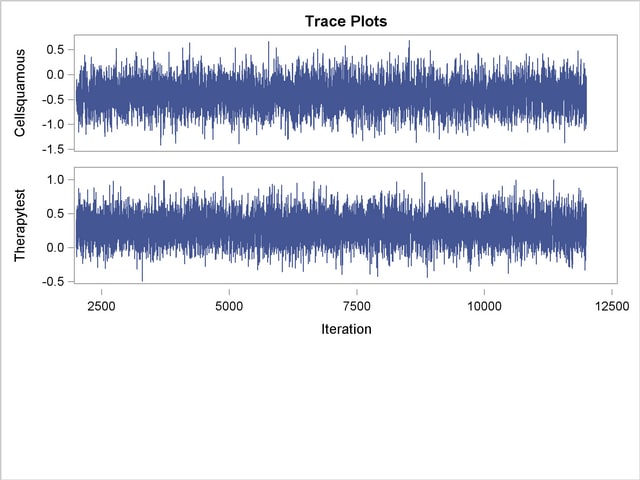
The first HAZARDRATIO statement compares the hazards between the standard therapy and the test therapy. Summaries of the posterior distribution of the corresponding hazard ratio are shown in Output 64.13.11. There is a 95% chance that the hazard ratio of standard therapy versus test therapy lies between 0.5 and 1.1.
The second HAZARDRATIO statement assesses the change of hazards for an increase in Age of 10 years. Summaries of the posterior distribution of the corresponding hazard ratio are shown in Output 64.13.12.
The third HAZARDRATIO statement compares the changes of hazards between two types of cells. For four types of cells, there are six different pairs of cell comparisons. The results are shown in Output 64.13.13.
| Hazard Ratio Statement 3: Hazard Ratios for Cell | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Description | N | Mean | Standard Deviation |
Quantiles | ||||||
| 25% | 50% | 75% | 95% Equal-Tail Interval | 95% HPD Interval | ||||||
| Cell adeno vs large | 10000 | 2.3048 | 0.7224 | 1.7929 | 2.1982 | 2.7000 | 1.2067 | 4.0227 | 1.0053 | 3.7057 |
| Cell adeno vs small | 10000 | 1.4377 | 0.4078 | 1.1522 | 1.3841 | 1.6704 | 0.7930 | 2.3999 | 0.7309 | 2.2662 |
| Cell adeno vs squamous | 10000 | 3.4449 | 1.0745 | 2.6789 | 3.2941 | 4.0397 | 1.8067 | 5.9727 | 1.6303 | 5.5946 |
| Cell large vs small | 10000 | 0.6521 | 0.1780 | 0.5264 | 0.6325 | 0.7545 | 0.3618 | 1.0588 | 0.3331 | 1.0041 |
| Cell large vs squamous | 10000 | 1.5579 | 0.4548 | 1.2344 | 1.4955 | 1.8089 | 0.8492 | 2.6346 | 0.7542 | 2.4575 |
| Cell small vs squamous | 10000 | 2.4728 | 0.7081 | 1.9620 | 2.3663 | 2.8684 | 1.3789 | 4.1561 | 1.2787 | 3.9263 |
|
|
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.