| The PHREG Procedure |
Assessment of the Proportional Hazards Model
The proportional hazards model specifies that the hazard function for the failure time  associated with a
associated with a 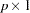 column covariate vector
column covariate vector  takes the form
takes the form
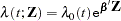 |
where 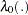 is an unspecified baseline hazard function and
is an unspecified baseline hazard function and 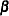 is a
is a 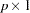 column vector of regression parameters. Lin, Wei, and Ying (1993) present graphical and numerical methods for model assessment based on the cumulative sums of martingale residuals and their transforms over certain coordinates (such as covariate values or follow-up times). The distributions of these stochastic processes under the assumed model can be approximated by the distributions of certain zero-mean Gaussian processes whose realizations can be generated by simulation. Each observed residual pattern can then be compared, both graphically and numerically, with a number of realizations from the null distribution. Such comparisons enable you to assess objectively whether the observed residual pattern reflects anything beyond random fluctuation. These procedures are useful in determining appropriate functional forms of covariates and assessing the proportional hazards assumption. You use the ASSESS statement to carry out these model-checking procedures.
column vector of regression parameters. Lin, Wei, and Ying (1993) present graphical and numerical methods for model assessment based on the cumulative sums of martingale residuals and their transforms over certain coordinates (such as covariate values or follow-up times). The distributions of these stochastic processes under the assumed model can be approximated by the distributions of certain zero-mean Gaussian processes whose realizations can be generated by simulation. Each observed residual pattern can then be compared, both graphically and numerically, with a number of realizations from the null distribution. Such comparisons enable you to assess objectively whether the observed residual pattern reflects anything beyond random fluctuation. These procedures are useful in determining appropriate functional forms of covariates and assessing the proportional hazards assumption. You use the ASSESS statement to carry out these model-checking procedures.
For a sample of  subjects, let
subjects, let 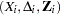 be the data of the
be the data of the  th subject; that is,
th subject; that is, 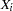 represents the observed failure time,
represents the observed failure time, 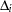 has a value of 1 if
has a value of 1 if 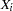 is an uncensored time and 0 otherwise, and
is an uncensored time and 0 otherwise, and 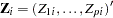 is a
is a  -vector of covariates. Let
-vector of covariates. Let  and
and 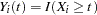 . Let
. Let
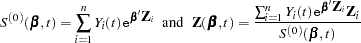 |
Let 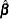 be the maximum partial likelihood estimate of
be the maximum partial likelihood estimate of 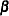 , and let
, and let 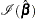 be the observed information matrix.
be the observed information matrix.
The martingale residuals are defined as
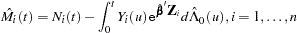 |
where 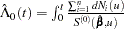 .
.
The empirical score process 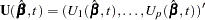 is a transform of the martingale residuals:
is a transform of the martingale residuals:
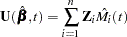 |
Checking the Functional Form of a Covariate
To check the functional form of the 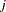 th covariate, consider the partial-sum process of
th covariate, consider the partial-sum process of 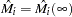 :
:
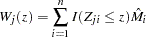 |
Under that null hypothesis that the model holds,  can be approximated by the zero-mean Gaussian process
can be approximated by the zero-mean Gaussian process
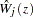 |
 |
 |
|||
 |
 |
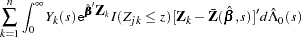 |
|||
 |
 |
 |
where 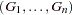 are independent standard normal variables that are independent of
are independent standard normal variables that are independent of 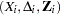 ,
, 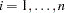 .
.
You can assess the functional form of the 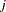 th covariate by plotting a small number of realizations (the default is 20) of
th covariate by plotting a small number of realizations (the default is 20) of 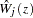 on the same graph as the observed
on the same graph as the observed  and visually comparing them to see how typical the observed pattern of
and visually comparing them to see how typical the observed pattern of  is of the null distribution samples. You can supplement the graphical inspection method with a Kolmogorov-type supremum test. Let
is of the null distribution samples. You can supplement the graphical inspection method with a Kolmogorov-type supremum test. Let 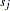 be the observed value of
be the observed value of 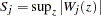 and let
and let 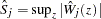 . The
. The  -value
-value  is approximated by
is approximated by 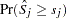 , which in turn is approximated by generating a large number of realizations (1000 is the default) of
, which in turn is approximated by generating a large number of realizations (1000 is the default) of 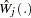 .
.
Checking the Proportional Hazards Assumption
Consider the standardized empirical score process for the 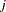 th component of
th component of 
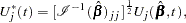 |
Under the null hypothesis that the model holds,  can be approximated by
can be approximated by
 |
 |
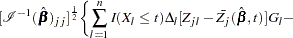 |
|||
 |
 |
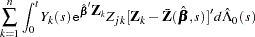 |
|||
 |
 |
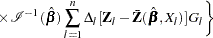 |
where 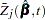 is the
is the 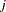 th component of
th component of 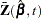 , and
, and 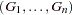 are independent standard normal variables that are independent of
are independent standard normal variables that are independent of 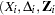 ,
,  .
.
You can assess the proportional hazards assumption for the 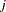 th covariate by plotting a few realizations of
th covariate by plotting a few realizations of 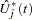 on the same graph as the observed
on the same graph as the observed  and visually comparing them to see how typical the observed pattern of
and visually comparing them to see how typical the observed pattern of  is of the null distribution samples. Again you can supplement the graphical inspection method with a Kolmogorov-type supremum test. Let
is of the null distribution samples. Again you can supplement the graphical inspection method with a Kolmogorov-type supremum test. Let 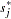 be the observed value of
be the observed value of 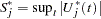 and let
and let 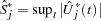 . The
. The  -value
-value 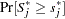 is approximated by
is approximated by  , which in turn is approximated by generating a large number of realizations (1000 is the default) of
, which in turn is approximated by generating a large number of realizations (1000 is the default) of 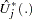 .
.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.