The MIANALYZE Procedure

Getting Started: MIANALYZE Procedure

Consider the following Fitness data set that has been altered to contain an arbitrary pattern of missingness:

    *----------------- Data on Physical Fitness -----------------*
    | These measurements were made on men involved in a physical |
    | fitness course at N.C. State University.                   |
    | Only selected variables of                                 |
    | Oxygen (oxygen intake, ml per kg body weight per minute),  |
    | Runtime (time to run 1.5 miles in minutes), and            |
    | RunPulse (heart rate while running) are used.              |
    | Certain values were changed to missing for the analysis.   |
    *------------------------------------------------------------*;
    data FitMiss;
       input Oxygen RunTime RunPulse @@;
       datalines;
    44.609  11.37  178     45.313  10.07  185
    54.297   8.65  156     59.571    .      .
    49.874   9.22    .     44.811  11.63  176
      .     11.95  176          .  10.85    .
    39.442  13.08  174     60.055   8.63  170
    50.541    .      .     37.388  14.03  186
    44.754  11.12  176     47.273    .      .
    51.855  10.33  166     49.156   8.95  180
    40.836  10.95  168     46.672  10.00    .
    46.774  10.25    .     50.388  10.08  168
    39.407  12.63  174     46.080  11.17  156
    45.441   9.63  164       .      8.92    .
    45.118  11.08    .     39.203  12.88  168
    45.790  10.47  186     50.545   9.93  148
    48.673   9.40  186     47.920  11.50  170
    47.467  10.50  170
    ;

Suppose that the data are multivariate normally distributed and that the missing data are missing at random (see the "Statistical Assumptions for Multiple Imputation" section in the chapter "The MI Procedure" for a description of these assumptions). The following statements use the MI procedure to impute missing values for the FitMiss data set:

   proc mi data=FitMiss noprint out=outmi seed=3237851;
      var Oxygen RunTime RunPulse;
   run;

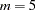The MI procedure creates imputed data sets, which are stored in the outmi data set. A variable named _Imputation_ indicates the imputation numbers. Based on $\text{[math]}$ imputations, $\text{[math]}$ different sets of the point and variance estimates for a parameter can be computed. In this example, $\text{[math]}$ is the default.

The following statements generate regression coefficients for each of the five imputed data sets:

   proc reg data=outmi outest=outreg covout noprint;
      model Oxygen= RunTime RunPulse;
      by _Imputation_;
   run;

The following statements display (in Figure 55.1) output parameter estimates and covariance matrices from PROC REG for the first two imputed data sets:

   proc print data=outreg(obs=8);
      var _Imputation_ _Type_ _Name_
         Intercept RunTime RunPulse;
      title 'Parameter Estimates from Imputed Data Sets';
   run;

Figure 55.1 Parameter Estimates

Parameter Estimates from Imputed Data Sets

Obs	_Imputation_	_TYPE_	_NAME_	Intercept	RunTime	RunPulse
1	1	PARMS		86.544	-2.82231	-0.05873
2	1	COV	Intercept	100.145	-0.53519	-0.55077
3	1	COV	RunTime	-0.535	0.10774	-0.00345
4	1	COV	RunPulse	-0.551	-0.00345	0.00343
5	2	PARMS		83.021	-3.00023	-0.02491
6	2	COV	Intercept	79.032	-0.66765	-0.41918
7	2	COV	RunTime	-0.668	0.11456	-0.00313
8	2	COV	RunPulse	-0.419	-0.00313	0.00264

The following statements combine the five sets of regression coefficients:

   proc mianalyze data=outreg;
      modeleffects Intercept RunTime RunPulse;
   run;

The "Model Information" table in Figure 55.2 lists the input data set(s) and the number of imputations.

Figure 55.2 Model Information Table

The MIANALYZE Procedure

Model Information
Data Set	WORK.OUTREG
Number of Imputations	5

The "Variance Information" table in Figure 55.3 displays the between-imputation, within-imputation, and total variances for combining complete-data inferences. It also displays the degrees of freedom for the total variance, the relative increase in variance due to missing values, the fraction of missing information, and the relative efficiency for each parameter estimate.

Figure 55.3 Variance Information Table

Variance Information
Parameter	Variance			DF	Relative Increase in Variance	Fraction Missing Information	Relative Efficiency
Parameter	Between	Within	Total	DF	Relative Increase in Variance	Fraction Missing Information	Relative Efficiency
Intercept	45.529229	76.543614	131.178689	23.059	0.713777	0.461277	0.915537
RunTime	0.019390	0.106220	0.129487	123.88	0.219051	0.192620	0.962905
RunPulse	0.001007	0.002537	0.003746	38.419	0.476384	0.355376	0.933641

The "Parameter Estimates" table in Figure 55.4 displays a combined estimate and standard error for each regression coefficient (parameter). Inferences are based on t distributions. The table displays a 95% confidence interval and a t test with the associated p-value for the hypothesis that the parameter is equal to the value specified with the THETA0= option (in this case, zero by default). The minimum and maximum parameter estimates from the imputed data sets are also displayed.

Figure 55.4 Parameter Estimates

Parameter Estimates
Parameter	Estimate	Std Error	95% Confidence Limits		DF	Minimum	Maximum	Theta0	t for H0: Parameter=Theta0	Pr > \|t\|
Intercept	90.837440	11.453327	67.14779	114.5271	23.059	83.020730	100.839807	0	7.93	<.0001
RunTime	-3.032870	0.359844	-3.74511	-2.3206	123.88	-3.204426	-2.822311	0	-8.43	<.0001
RunPulse	-0.068578	0.061204	-0.19243	0.0553	38.419	-0.112840	-0.024910	0	-1.12	0.2695

Top of Page