| The LOGISTIC Procedure |
| Scoring Data Sets |
Scoring a data set, which is especially important for predictive modeling, means applying a previously fitted model to a new data set in order to compute the conditional, or posterior, probabilities of each response category given the values of the explanatory variables in each observation.
The SCORE statement enables you to score new data sets and output the scored values and, optionally, the corresponding confidence limits into a SAS data set. If the response variable is included in the new data set, then you can request fit statistics for the data, which is especially useful for test or validation data. If the response is binary, you can also create a SAS data set containing the receiver operating characteristic (ROC) curve. You can specify multiple SCORE statements in the same invocation of PROC LOGISTIC.
By default, the posterior probabilities are based on implicit prior probabilities that are proportional to the frequencies of the response categories in the training data (the data used to fit the model). Explicit prior probabilities should be specified when the sample proportions of the response categories in the training data differ substantially from the operational data to be scored. For example, to detect a rare category, it is common practice to use a training set in which the rare categories are overrepresented; without prior probabilities that reflect the true incidence rate, the predicted posterior probabilities for the rare category will be too high. By specifying the correct priors, the posterior probabilities are adjusted appropriately.
The model fit to the DATA= data set in the PROC LOGISTIC statement is the default model used for the scoring. Alternatively, you can save a model fit in one run of PROC LOGISTIC and use it to score new data in a subsequent run. The OUTMODEL= option in the PROC LOGISTIC statement saves the model information in a SAS data set. Specifying this data set in the INMODEL= option of a new PROC LOGISTIC run will score the DATA= data set in the SCORE statement without refitting the model.
Posterior Probabilities and Confidence Limits
Let 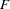 be the inverse link function. That is,
be the inverse link function. That is,
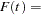 |
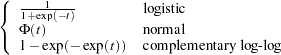 |
The first derivative of 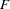 is given by
is given by
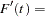 |
 |
Suppose there are 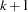 response categories. Let Y be the response variable with levels
response categories. Let Y be the response variable with levels 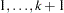 . Let
. Let 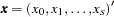 be a
be a 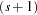 -vector of covariates, with
-vector of covariates, with  . Let
. Let 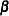 be the vector of intercept and slope regression parameters.
be the vector of intercept and slope regression parameters.
Posterior probabilities are given by
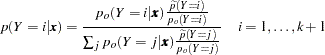 |
where the old posterior probabilities (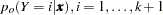 ) are the conditional probabilities of the response categories given
) are the conditional probabilities of the response categories given  , and the old priors (
, and the old priors (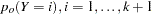 ) are the sample proportions of response categories of the training data. To simplify notation, absorb the old priors into the new priors; that is
) are the sample proportions of response categories of the training data. To simplify notation, absorb the old priors into the new priors; that is
 |
The posterior probabilities are functions of 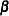 and their estimates are obtained by substituting
and their estimates are obtained by substituting 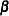 by its MLE
by its MLE 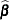 . The variances of the estimated posterior probabilities are given by the delta method as follows:
. The variances of the estimated posterior probabilities are given by the delta method as follows:
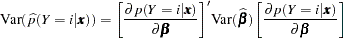 |
where
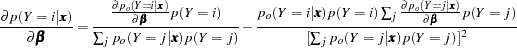 |
and the old posterior probabilities 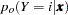 are described in the following sections.
are described in the following sections.
A 100( )% confidence interval for
)% confidence interval for 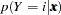 is
is
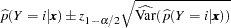 |
where 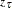 is the upper 100
is the upper 100 percentile of the standard normal distribution.
percentile of the standard normal distribution.
Binary and Cumulative Response Models
Let 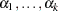 be the intercept parameters and let
be the intercept parameters and let 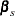 be the vector of slope parameters. Denote
be the vector of slope parameters. Denote 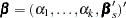 . Let
. Let
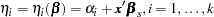 |
Estimates of 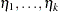 are obtained by substituting the maximum likelihood estimate
are obtained by substituting the maximum likelihood estimate 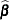 for
for 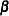 .
.
The predicted probabilities of the responses are
 |
For 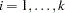 , let
, let 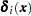 be a (
be a (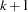 ) column vector with
) column vector with  th entry equal to 1,
th entry equal to 1, 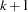 th entry equal to
th entry equal to  , and all other entries 0. The derivative of
, and all other entries 0. The derivative of 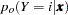 with respect to
with respect to 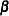 are
are
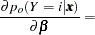 |
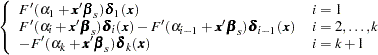 |
The cumulative posterior probabilities are
 |
Their derivatives are
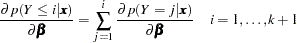 |
In the delta-method equation for the variance, replace 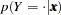 with
with 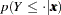 .
.
Finally, for the cumulative response model, use
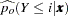 |
 |
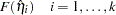 |
|||
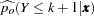 |
 |
 |
|||
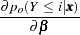 |
 |
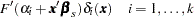 |
|||
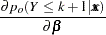 |
 |
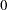 |
Generalized Logit Model
Consider the last response level (Y=k+1) as the reference. Let 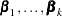 be the (intercept and slope) parameter vectors for the first
be the (intercept and slope) parameter vectors for the first 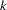 logits, respectively. Denote
logits, respectively. Denote 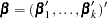 . Let
. Let 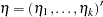 with
with
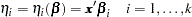 |
Estimates of 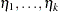 are obtained by substituting the maximum likelihood estimate
are obtained by substituting the maximum likelihood estimate 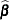 for
for 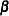 .
.
The predicted probabilities are
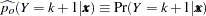 |
 |
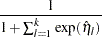 |
|||
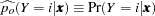 |
 |
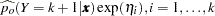 |
The derivative of 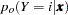 with respect to
with respect to 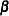 are
are
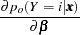 |
 |
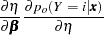 |
|||
 |
 |
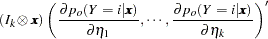 |
where
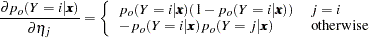 |
Special Case of Binary Response Model with No Priors
Let 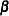 be the vector of regression parameters. Let
be the vector of regression parameters. Let
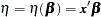 |
The variance of 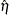 is given by
is given by
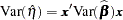 |
A 100( ) percent confidence interval for
) percent confidence interval for 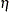 is
is
 |
Estimates of 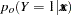 and confidence intervals for the
and confidence intervals for the 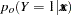 are obtained by back-transforming
are obtained by back-transforming 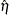 and the confidence intervals for
and the confidence intervals for 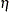 , respectively. That is,
, respectively. That is,
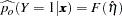 |
and the confidence intervals are
 |
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.