| Shared Concepts and Topics |
Truncated Power Function Basis
A truncated power function for a knot 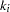 is a function defined by
is a function defined by
 |
Figure 18.1 shows such functions for  and
and 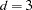 with a knot at
with a knot at  .
.


The name is derived from the fact that these functions are shifted power functions that get truncated to zero to the left of the knot. These functions are piecewise polynomial functions with two pieces whose function values and derivatives of all orders up to  are zero at the defining knot. Hence these functions are splines of degree
are zero at the defining knot. Hence these functions are splines of degree 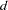 . It is easy to see that these
. It is easy to see that these  functions are linearly independent. However, they do not form a basis, because such a basis requires
functions are linearly independent. However, they do not form a basis, because such a basis requires 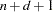 functions. The usual way to add
functions. The usual way to add  additional basis functions is to use the polynomials
additional basis functions is to use the polynomials  . These
. These  functions together with the
functions together with the  truncated power functions
truncated power functions 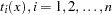 form the truncated power basis.
form the truncated power basis.
Note that each time a knot is repeated, the associated exponent used in the corresponding basis function is reduced by 1. For example, for splines of degree 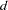 with 3 repeated knots
with 3 repeated knots  the corresponding basis functions are
the corresponding basis functions are 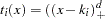 ,
,  , and
, and 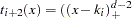 . Provided that the multiplicity of each repeated knot is less than or equal to the degree, this construction continues to yield a basis for the associated space of splines.
. Provided that the multiplicity of each repeated knot is less than or equal to the degree, this construction continues to yield a basis for the associated space of splines.
The main advantage of the truncated power function basis is the simplicity of its construction and the ease of interpreting the parameters in a model corresponding to these basis functions. However, there are two weaknesses when you use this basis for regression. These functions grow rapidly without bound as  increases, resulting in numerical precision problems when the
increases, resulting in numerical precision problems when the  data span a wide range. Furthermore, many or even all of these basis functions can be nonzero when evaluated at some
data span a wide range. Furthermore, many or even all of these basis functions can be nonzero when evaluated at some  value, resulting in a design matrix with few zeros that precludes the use of sparse matrix technology to speed up computation. This weakness can be addressed by using a B-spline basis.
value, resulting in a design matrix with few zeros that precludes the use of sparse matrix technology to speed up computation. This weakness can be addressed by using a B-spline basis.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.