| Introduction to Categorical Data Analysis Procedures |
| Stratified Simple Random Sampling: Multiple Populations |
Suppose you take two simple random samples, 50 men and 50 women, and ask the same question as before. You are now sampling two different populations that may have different response probabilities. The data can be tabulated as shown in Table 8.2.
Favorite Color |
||||
|---|---|---|---|---|
Sex |
Red |
Blue |
Green |
Total |
Male |
30 |
10 |
10 |
50 |
Female |
20 |
10 |
20 |
50 |
Total |
50 |
20 |
30 |
100 |
Note that the row marginal totals (50, 50) of the contingency table are fixed by the sampling design, but the column marginal totals (50, 20, 30) are random. There are six probabilities of interest for this table, and they are estimated by the sample proportions
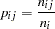 |
where 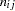 denotes the frequency for the
denotes the frequency for the  th population and the
th population and the 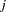 th response and
th response and 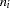 is the total frequency for the
is the total frequency for the  th population. For this contingency table, the sample proportions are shown in Table 8.3.
th population. For this contingency table, the sample proportions are shown in Table 8.3.
Favorite Color |
||||
|---|---|---|---|---|
Sex |
Red |
Blue |
Green |
Total |
Male |
0.60 |
0.20 |
0.20 |
1.00 |
Female |
0.40 |
0.20 |
0.40 |
1.00 |
The probability distribution of the six frequencies is the product multinomial distribution
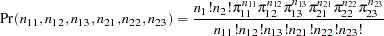 |
where 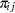 is the true probability of observing the
is the true probability of observing the 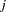 th response level in the
th response level in the  th population. The product multinomial distribution is simply the product of two or more individual multinomial distributions since the populations are independent. This distribution can be generalized to any number of populations and response levels.
th population. The product multinomial distribution is simply the product of two or more individual multinomial distributions since the populations are independent. This distribution can be generalized to any number of populations and response levels.
Stratified simple random sampling is the type of sampling required by the modeling procedures when there is more than one population. The product multinomial distribution is used to estimate a probability vector and its covariance matrix. If the sample sizes are sufficiently large, then the probability vector is approximately normally distributed as a result of central limit theory, and this result is used to compute appropriate test statistics for the specified statistical model. The statistics are known as Wald statistics, and they are approximately distributed as chi-square when the null hypothesis is true.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.