| The GLM Procedure |
| ODS Graphics |
This section describes the use of ODS for creating statistical graphs with the GLM procedure. To request these graphs you must specify the ODS GRAPHICS statement with an appropriate model, as discussed in the following list. For more information about the ODS GRAPHICS statement, see Chapter 21, Statistical Graphics Using ODS.
When the ODS Graphics are in effect, then for particular models the GLM procedure will produce default graphics.
If you specify a one-way analysis of variance model, with just one CLASS variable, the GLM procedure will produce a grouped box plot of the response values versus the CLASS levels. For an example of the box plot, see the section One-Way Layout with Means Comparisons.
If you specify a two-way analysis of variance model, with just two CLASS variables, the GLM procedure will produce an interaction plot of the response values, with horizontal position representing one CLASS variable and marker style representing the other; and with predicted response values connected by lines representing the two-way analysis. For an example of the interaction plot, see the section PROC GLM for Unbalanced ANOVA.
If you specify a model with a single continuous predictor, the GLM procedure will produce a fit plot of the response values versus the covariate values, with a curve representing the fitted relationship. For an example of the fit plot, see the section PROC GLM for Quadratic Least Squares Regression.
If you specify a model with a two continuous predictors and no CLASS variables, the GLM procedure will produce a panel of fit plots as in the single predictor case, with a plot of the response values versus one of the covariates at each of several values of the other covariate.
If you specify an analysis of covariance model, with one or two CLASS variables and one continuous variable, the GLM procedure will produce an analysis of covariance plot of the response values versus the covariate values, with lines representing the fitted relationship within each classification level. For an example of the analysis of covariance plot, see Example 39.4.
If you specify an LSMEANS statement with the PDIFF option, the GLM procedure will produce a plot appropriate for the type of LS-means comparison. For PDIFF=ALL (which is the default if you specify only PDIFF), the procedure produces a diffogram, which displays all pairwise LS-means differences and their significance. The display is also known as a "mean-mean scatter plot" (Hsu 1996). For PDIFF=CONTROL, the procedure produces a display of each noncontrol LS-mean compared to the control LS-mean, with two-sided confidence intervals for the comparison. For PDIFF=CONTROLL and PDIFF=CONTROLU a similar display is produced, but with one-sided confidence intervals. Finally, for the PDIFF=ANOM option, the procedure produces an "analysis of means" plot, comparing each LS-mean to the average LS-mean.
If you specify a MEANS statement, the GLM procedure will produce a grouped box plot of the response values versus the effect for which means are being calculated.
In addition to the default graphics mentioned previously, you can request plots that help you diagnose the quality of the fitted model.
The PLOTS=DIAGNOSTICS option in the PROC GLM statement requests that a panel of summary diagnostics for the fit be displayed. The panel displays scatter plots of residuals, absolute residuals, studentized residuals, and observed responses by predicted values; studentized residuals by leverage; Cook’s
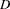 by observation; a Q-Q plot of residuals; a residual histogram; and a residual-fit spread plot.
by observation; a Q-Q plot of residuals; a residual histogram; and a residual-fit spread plot. The PLOTS=RESIDUALS option in the PROC GLM statement requests scatter plots of the residuals against each continuous covariate.
ODS Graph Names
PROC GLM assigns a name to each graph it creates using ODS. You can use these names to reference the graphs when using ODS. The names are listed in Table 39.9.
To request these graphs you must specify the ODS Graphics statement. For more information about the ODS GRAPHICS statement, see Chapter 21, Statistical Graphics Using ODS.
ODS Graph Name |
Plot Description |
Option |
|---|---|---|
ANCOVAPlot |
Analysis of covariance plot |
Analysis of covariance model |
ANOMPlot |
Plot of LS-mean differences against average LS-mean |
|
BoxPlot |
Box plot of group means |
One-way ANOVA model or MEANS statement |
ContourFit |
Plot of predicted response surface |
Two-predictor response surface model |
ControlPlot |
Plot of LS-mean differences against a control level |
|
DiagnosticsPanel |
Panel of summary diagnostics for the fit |
PLOTS=DIAGNOSTICS |
CooksDPlot |
Cook’s |
PLOTS=DIAGNOSTICS(UNPACK) |
ObservedByPredicted |
Observed by predicted |
PLOTS=DIAGNOSTICS(UNPACK) |
QQPlot |
Residual Q-Q plot |
PLOTS=DIAGNOSTICS(UNPACK) |
ResidualByPredicted |
Residual by predicted values |
PLOTS=DIAGNOSTICS(UNPACK) |
ResidualHistogram |
Residual histogram |
PLOTS=DIAGNOSTICS(UNPACK) |
RFPlot |
RF plot |
PLOTS=DIAGNOSTICS(UNPACK) |
RStudentByPredicted |
Studentized residuals by predicted |
PLOTS=DIAGNOSTICS(UNPACK) |
RStudentByLeverage |
RStudent by hat diagonals |
PLOTS=DIAGNOSTICS(UNPACK) |
DiffPlot |
Plot of LS-mean pairwise differences |
|
IntPlot |
Interaction plot |
Two-way ANOVA model |
FitPlot |
Plot of predicted response by predictor |
Model with one continuous predictor |
ResidualPlots |
Plots of the residuals against each continuous covariate |
PLOTS=RESIDUALS |
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.