In the GAM procedure, curvewise confidence intervals for smoothing splines and pointwise confidence intervals for loess are provided in the output data set.

Curvewise Confidence Interval for Smoothing Spline

Viewing the spline model as a Bayesian model, Wahba (1983) proposes Bayesian confidence intervals for smoothing spline estimates as follows:

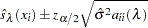where is the th diagonal element of the matrix and 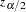is the 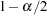quantile of the standard normal distribution. The confidence intervals are interpreted as intervals "across the function" as opposed to pointwise intervals.

Suppose that you fit a spline estimate to experimental data that consists of a true function 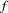and a random error term, 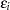. In repeated experiments, it is likely that about 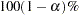of the confidence intervals cover the corresponding true values, although some values are covered every time and other values are not covered by the confidence intervals most of the time. This effect is more pronounced when the true response curve or surface has small regions of particularly rapid change.

Pointwise Confidence Interval for Loess Smoothers

As defined in Cleveland, Devlin, and Grosse (1988), a standardized residual for a loess smoother follows a distribution with degrees of freedom, where is called the "lookup degrees of freedom," defined as

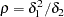where 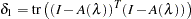and 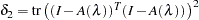. Therefore an approximate pointwise confidence interval at 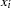is

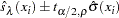where is the 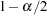quantile of the distribution with degrees of freedom and 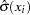is the estimate of the standard deviation.