| The DISTANCE Procedure |
Example 32.2 Financial Data – Stock Dividends
The following data set contains the average dividend yields for 15 utility stocks in the United States. The observations are names of the companies, and the variables correspond to the annual dividend yields for the period 1986–1990. The objective is to group similar stocks into clusters.
Before the cluster analysis is performed, the correlation similarity is chosen for measuring the closeness between each observation. Since distance type of measures are required by the CLUSTER procedure, METHOD=DCORR is used in the PROC DISTANCE statement to transform the correlation measures to the distance measures. Notice that in Output 32.2.1, all the values in the distance matrix are between 0 and 2.
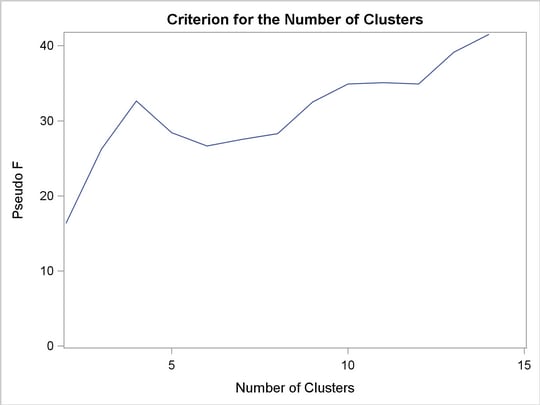
The macro function DO_CLUSTER performs cluster analysis and presents the results in graphs. The CLUSTER procedure performs hierarchical clustering by using agglomerative methods based on the distance data created from the previous PROC DISTANCE statement. The resulting tree diagrams can be saved into an output data set and can later be plotted by the TREE procedure. Since the CCC statistic is not suitable for distance type of data, only the Pseudo statistic is requested to identify the number of clusters.
Two clustering methods are invoked in the DO_CLUSTER macro: Ward’s and the average linkage methods. Since the results of the Pseudo  statistic from both Ward’s and the average linkage methods contain many missing values, only the plot of the Pseudo
statistic from both Ward’s and the average linkage methods contain many missing values, only the plot of the Pseudo 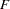 statistic versus the number of clusters is requested by specifying PLOTS(ONLY)= PSF in the PROC CLUSTER statement.
statistic versus the number of clusters is requested by specifying PLOTS(ONLY)= PSF in the PROC CLUSTER statement.
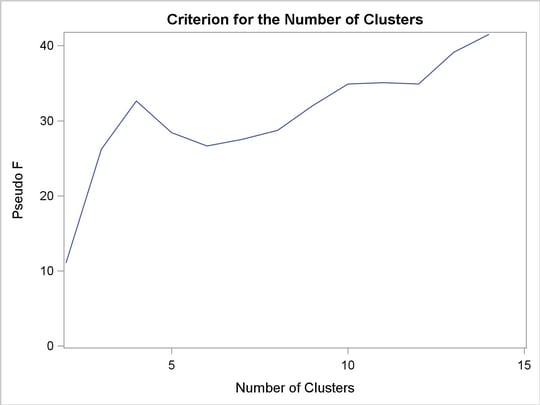
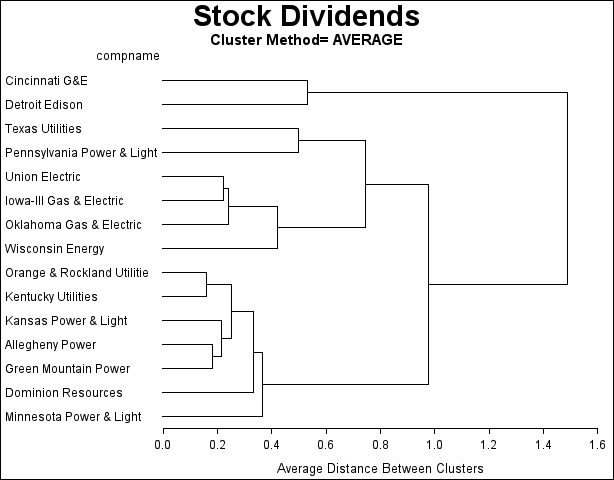
Both Output 32.2.2 and Output 32.2.3 suggest a possible clusters of 4. Both methods produce the same clustering result, as shown in Output 32.2.4 and Output 32.2.5. The four clusters are as follows:
Cincinnati G&E and Detroit Edison
Texas Utilities and Pennsylvania Power & Light
Union Electric, Iowa-Ill Gas & Electric, Oklahoma Gas & Electric, and Wisconsin Energy
Orange & Rockland Utilities, Kentucky Utilities, Kansas Power & Light, Allegheny Power, Green Mountain Power, Dominion Resources, and Minnesota Power & Light
data stock;
title 'Stock Dividends';
input compname &$26. div_1986 div_1987 div_1988
div_1989 div_1990;
datalines;
Cincinnati G&E 8.4 8.2 8.4 8.1 8.0
Texas Utilities 7.9 8.9 10.4 8.9 8.3
Detroit Edison 9.7 10.7 11.4 7.8 6.5
Orange & Rockland Utilities 6.5 7.2 7.3 7.7 7.9
Kentucky Utilities 6.5 6.9 7.0 7.2 7.5
Kansas Power & Light 5.9 6.4 6.9 7.4 8.0
Union Electric 7.1 7.5 8.4 7.8 7.7
Dominion Resources 6.7 6.9 7.0 7.0 7.4
Allegheny Power 6.7 7.3 7.8 7.9 8.3
Minnesota Power & Light 5.6 6.1 7.2 7.0 7.5
Iowa-Ill Gas & Electric 7.1 7.5 8.5 7.8 8.0
Pennsylvania Power & Light 7.2 7.6 7.7 7.4 7.1
Oklahoma Gas & Electric 6.1 6.7 7.4 6.7 6.8
Wisconsin Energy 5.1 5.7 6.0 5.7 5.9
Green Mountain Power 7.1 7.4 7.8 7.8 8.3
;
proc distance data=stock method=dcorr out=distdcorr;
var interval(div_1986 div_1987 div_1988 div_1989 div_1990);
id compname;
run;
proc print data=distdcorr;
id compname;
title2 'Distance Matrix for 15 Utility Stocks';
run;
title2;
/* performs cluster analysis and plots the results */
%macro do_cluster(clusmtd);
%let clusmtd = %upcase(&clusmtd);
title2 "Cluster Method= &clusmtd";
/* compute pseudo statistic versus number of cluster and get plot */
proc cluster data=distdcorr method=&clusmtd outtree=Tree
pseudo plots(only)= psf;
id compname;
run;
/* plot tree diagram */
proc tree data=Tree horizontal;
id compname;
run;
%mend;
ods graphics on; /* METHOD=WARD */ %do_cluster(ward);
/* METHOD=AVERAGE */ %do_cluster(average); ods graphics off;
| Stock Dividends |
| Distance Matrix for 15 Utility Stocks |
| compname | Cincinnati_G_E | Texas_Utilities | Detroit_Edison | Orange___Rockland_Utilitie | Kentucky_Utilities | Kansas_Power___Light | Union_Electric | Dominion_Resources | Allegheny_Power | Minnesota_Power___Light | Iowa_Ill_Gas___Electric | Pennsylvania_Power___Light | Oklahoma_Gas___Electric | Wisconsin_Energy | Green_Mountain_Power |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cincinnati G&E | 0.00000 | . | . | . | . | . | . | . | . | . | . | . | . | . | . |
| Texas Utilities | 0.82056 | 0.00000 | . | . | . | . | . | . | . | . | . | . | . | . | . |
| Detroit Edison | 0.40511 | 0.65453 | 0.00000 | . | . | . | . | . | . | . | . | . | . | . | . |
| Orange & Rockland Utilitie | 1.35380 | 0.88583 | 1.27306 | 0.00000 | . | . | . | . | . | . | . | . | . | . | . |
| Kentucky Utilities | 1.35581 | 0.92539 | 1.29382 | 0.12268 | 0.00000 | . | . | . | . | . | . | . | . | . | . |
| Kansas Power & Light | 1.34227 | 0.94371 | 1.31696 | 0.19905 | 0.12874 | 0.00000 | . | . | . | . | . | . | . | . | . |
| Union Electric | 0.98516 | 0.29043 | 0.89048 | 0.68798 | 0.71824 | 0.72082 | 0.00000 | . | . | . | . | . | . | . | . |
| Dominion Resources | 1.32945 | 0.96853 | 1.29016 | 0.33290 | 0.21510 | 0.24189 | 0.76587 | 0.00000 | . | . | . | . | . | . | . |
| Allegheny Power | 1.30492 | 0.81666 | 1.24565 | 0.17844 | 0.15759 | 0.17029 | 0.58452 | 0.27819 | 0.00000 | . | . | . | . | . | . |
| Minnesota Power & Light | 1.24069 | 0.74082 | 1.20432 | 0.32581 | 0.30462 | 0.27231 | 0.48372 | 0.35733 | 0.15615 | 0.00000 | . | . | . | . | . |
| Iowa-Ill Gas & Electric | 1.04924 | 0.43100 | 0.97616 | 0.61166 | 0.61760 | 0.61736 | 0.16923 | 0.63545 | 0.47900 | 0.36368 | 0.00000 | . | . | . | . |
| Pennsylvania Power & Light | 0.74931 | 0.37821 | 0.44256 | 1.03566 | 1.08878 | 1.12876 | 0.63285 | 1.14354 | 1.02358 | 0.99384 | 0.75596 | 0.00000 | . | . | . |
| Oklahoma Gas & Electric | 1.00604 | 0.30141 | 0.86200 | 0.68021 | 0.70259 | 0.73158 | 0.17122 | 0.72977 | 0.58391 | 0.50744 | 0.19673 | 0.60216 | 0.00000 | . | . |
| Wisconsin Energy | 1.17988 | 0.54830 | 1.03081 | 0.45013 | 0.47184 | 0.53381 | 0.37405 | 0.51969 | 0.37522 | 0.36319 | 0.30259 | 0.76085 | 0.28070 | 0.00000 | . |
| Green Mountain Power | 1.30397 | 0.88063 | 1.27176 | 0.26948 | 0.17909 | 0.15377 | 0.64869 | 0.17360 | 0.13958 | 0.19370 | 0.52083 | 1.09269 | 0.64175 | 0.44814 | 0 |
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.