Previous Page

|

Next Page

The CATMOD Procedure

Example 28.11 Predicted Probabilities

Suppose you have collected marketing research data to examine the relationship between a prospect’s likelihood of buying your product and the person’s education and income. Specifically, the variables are as follows:

Variable	Levels	Interpretation
Education	high, low	prospect’s education level
Income	high, low	prospect’s income level
Purchase	yes, no	Did prospect purchase product?

The following statements first create a data set, loan, that contains the marketing research data. Then the CATMOD procedure fits a model, obtains the parameter estimates, and obtains the predicted probabilities of interest. These statements produce Output 28.11.1 and Output 28.11.2.

   data loan;
      input Education $ Income $ Purchase $ wt;
      datalines;
   high  high  yes    54
   high  high  no     23
   high  low   yes    41
   high  low   no     12
   low   high  yes    35
   low   high  no     42
   low   low   yes    19
   low   low   no      8
   ;

   ods output PredictedValues=Predicted (keep=Education Income PredFunction);
   proc catmod data=loan order=data;
      weight wt;
      response marginals;
      model Purchase=Education Income / pred design;
   run;

   proc sort data=Predicted;
      by descending PredFunction;
   run;
   proc print data=Predicted;
   run;

Notice that the preceding statements use the Output Delivery System (ODS) to output the parameter estimates instead of the OUT= option, though either can be used.

Output 28.11.1 Marketing Research Data: Obtaining Predicted Probabilities

Complex Sample Survey Analysis

The CATMOD Procedure

Data Summary
Response	Purchase	Response Levels	2
Weight Variable	wt	Populations	4
Data Set	LOAN	Total Frequency	234
Frequency Missing	0	Observations	8

Population Profiles
Sample	Education	Income	Sample Size
1	high	high	77
2	high	low	53
3	low	high	77
4	low	low	27

Response Profiles
Response	Purchase
1	yes
2	no

Response Functions and Design Matrix
Sample	Response Function	Design Matrix
		1	2	3
1	0.70130	1	1	1
2	0.77358	1	1	-1
3	0.45455	1	-1	1
4	0.70370	1	-1	-1

Analysis of Variance
Source	DF	Chi-Square	Pr > ChiSq
Intercept	1	418.36	<.0001
Education	1	8.85	0.0029
Income	1	4.70	0.0302
Residual	1	1.84	0.1745

Analysis of Weighted Least Squares Estimates
Parameter		Estimate	Standard Error	Chi- Square	Pr > ChiSq
Intercept		0.6481	0.0317	418.36	<.0001
Education	high	0.0924	0.0311	8.85	0.0029
Income	high	-0.0675	0.0312	4.70	0.0302

Predicted Values for Response Functions
Education	Income	Function Number	Observed		Predicted		Residual
			Function	Standard Error	Function	Standard Error
high	high	1	0.701299	0.052158	0.67294	0.047794	0.028359
high	low	1	0.773585	0.057487	0.808034	0.051586	-0.03445
low	high	1	0.454545	0.056744	0.48811	0.051077	-0.03356
low	low	1	0.703704	0.087877	0.623204	0.064867	0.080499

You can use the predicted values (values of PredFunction in Output 28.11.2) as scores representing the likelihood that a randomly chosen subject from one of these populations will purchase the product. Notice that the "Response Profiles" table in Output 28.11.1 shows you that the first sorted level of Purchase is 'yes', indicating that the predicted probabilities are for Pr(Purchase='yes'). For example, someone with high education and low income has an estimated probability of purchase of 0.808. Like any response function estimate given by PROC CATMOD, this estimate can be obtained by cross-multiplying the row from the design matrix corresponding to the sample (sample number 2 in this case) with the vector of parameter estimates: .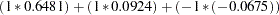

This ranking of scores can help in decision making (for example, with respect to allocation of advertising dollars, choice of advertising media, choice of print media, and so on).

Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.