The RAM statement defines the elements of the symmetric RAM matrix model

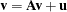in the form of a list type input (McArdle and McDonald 1984).

The covariance structure is given by

with selection matrix 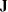and

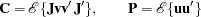You can specify only one RAM statement with each PROC CALIS statement. Using the RAM statement requires that the first variable numbers in the path diagram and in the vector correspond to the numbers of the manifest variables of the given covariance or correlation matrix. If you are not sure what the order of the manifest variables in the DATA= data set is, use a VAR statement to specify the order of these observed variables. Using the AUGMENT option includes the INTERCEPT variable as a manifest variable with number 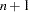in the RAM model. In this case, latent variables have to start with 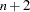. The box of each manifest variable in the path diagram is assigned the number of the variable in the covariance or correlation matrix.

The selection matrix 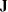is always a rectangular identity (IDE) matrix, and it does not have to be specified in the RAM statement.

A constant matrix element is defined in a RAM statement by a list-entry with four numbers. You define a parameter element by three or four numbers followed by a name for the parameter. Separate the list entries with a comma. Each list-entry in the RAM statement corresponds to a path in the diagram, as follows:

• The first number in each list entry (matrix-number) is the number of arrowheads of the path, which is the same as the number of the matrix in the RAM model (1 := 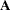, 2 := ).

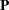• The second number in each list entry (row-number) is the number of the node in the diagram to which the path points, which is the same as the row number of the matrix element.

• The third number in each list entry (column-number) is the number of the node in the diagram from which the path originates, which is the same as the column number of the matrix element.

• The fourth number (value) gives the (initial) value of the path coefficient. If you do not specify a fifth list-entry, this number specifies a constant coefficient; otherwise, this number specifies the initial value of this parameter. It is not necessary to specify the fourth item. If you specify neither the fourth nor the fifth item, the constant is set to 1 by default. If the fourth item (value) is not specified for a parameter, PROC CALIS tries to compute an initial value for this parameter.

• If the path coefficient is a parameter rather than a constant, then a fifth item in the list entry (parameter-name) is required to assign a name to the parameter. Using the same name for different paths constrains the corresponding coefficients to be equal.

If the initial value of a parameter is not specified in the list, the initial value is chosen in one of the following ways:

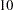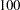• If the PROC CALIS statement contains a RANDOM= option, then the parameter obtains a randomly generated initial value , such that . The uninitialized parameters in the diagonals of the central model matrices are given the random values multiplied by , , or the value specified in the DEMPHAS= option.

• If the RANDOM= option is not used, PROC CALIS tries to estimate the initial values.

• If the initial values cannot be estimated, the value of the START= option is used as an initial value.

If your model contains many unconstrained parameters and it is too cumbersome to find different parameter names, you can specify all those parameters by the same prefix name. A prefix is a short name followed by a colon. The CALIS procedure then generates a parameter name by appending an integer suffix to this prefix name. The prefix name should have no more than five or six characters so that the generated parameter name is not longer than eight characters. To avoid unintentional equality constraints, the prefix names should not coincide with explicitly defined parameter names.

For example, consider the following model described in the section Specifying a Second-Order Factor-Analysis Model:

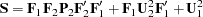You can fit this model by using the following RAM model statement:

   ram
      1  1 10    x1,
      1  2 10    x2,
      1  3 10    x3,
      1  4 11    x4,
      1  5 11    x5,
      1  6 11    x6,
      1  7 12    x7,
      1  8 12    x8,
      1  9 12    x9,
      1 10 13    y1,
      1 11 13    y1,
      1 11 14    y2,
      1 12 14    y2,
      2  1  1    u:,
      2  2  2    u:,
      2  3  3    u:,
      2  4  4    u:,
      2  5  5    u:,
      2  6  6    u:,
      2  7  7    u:,
      2  8  8    u:,
      2  9  9    u:,
      2 10 10    v:,
      2 11 11    v:,
      2 12 12    v:,
      2 13 13    p ,
      2 14 14    p ;
   run;

The confirmatory second-order factor analysis model corresponds to the path diagram displayed in Figure 25.3.

Figure 25.3 Path Diagram of Second-Order Factor Analysis Model

There is a very close relationship between the RAM model algebra and the specification of structural linear models by path diagrams. See Figure 25.4 for an example.

Figure 25.4 Examples of RAM Nomography

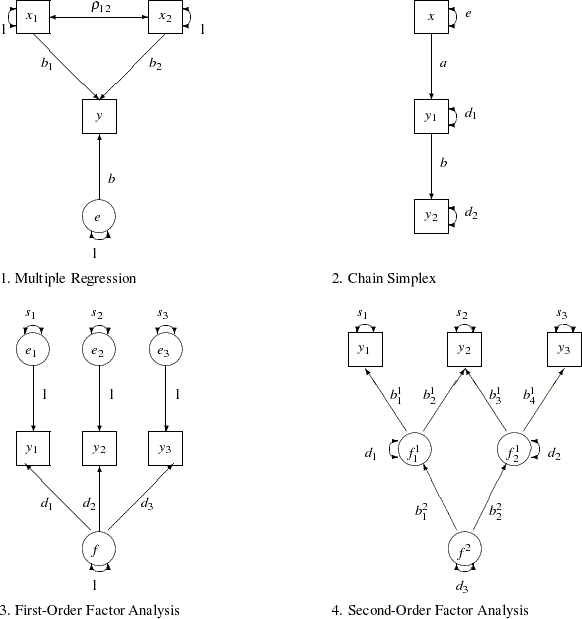
Refer to McArdle (1980) for the interpretation of the models displayed in Figure 25.4.