| The CALIS Procedure |
| NLOPTIONS Statement |
Many options that are available in PROC NLP can now be specified for the optimization subroutines in PROC CALIS by using the NLOPTIONS statement. The NLOPTIONS statement provides more displayed and file output on the results of the optimization process, and it permits the same set of termination criteria as in PROC NLP. These are more technical options that you might not need to specify in most cases. The available options are summarized in Table 25.2 through Table 25.4, and the options are described in detail in the following three sections.
Option |
Description |
|---|---|
Estimation Methods |
|
G4=i |
specifies the algorithm for computing standard errors |
Optimization Techniques |
|
FCONV=r |
specifies the relative change function convergence criterion |
GCONV=r |
specifies the relative gradient convergence criterion |
INSTEP=r |
specifies the initial step length (SALPHA=, RADIUS=) |
LINESEARCH=i |
specifies the line-search method |
LSPRECISION=r |
specifies the line-search precision |
MAXFUNC=i |
specifies the maximum number of function calls |
MAXITER=i <n> |
specifies the maximum number of iterations |
TECHNIQUE=name |
specifies the minimization method |
UPDATE=name |
specifies the update technique |
Miscellaneous Options |
|
ASINGULAR=r |
specifies the absolute singularity criterion for inversion of the information matrix |
COVSING=r |
specifies the singularity tolerance of the information matrix |
MSINGULAR=r |
specifies the relative M singularity criterion for inversion of the information matrix |
SINGULAR=r |
specifies the singularity criterion for inversion of the Hessian |
VSINGULAR=r |
specifies the relative V singularity criterion for inversion of the information matrix |
Option |
Description |
|---|---|
Options Used by All Techniques |
|
ABSCONV=r |
specifies the absolute function convergence criterion |
MAXFUNC=i |
specifies the maximum number of function calls |
MAXITER=i <n> |
specifies the maximum number of iterations |
MAXTIME=r |
specifies the maximum CPU time |
MINITER=i |
specifies the minimum number of iterations |
Options for Unconstrained and Linearly Constrained Techniques |
|
ABSFCONV=r <n> |
specifies the absolute change function convergence criterion |
ABSGCONV=r <n> |
specifies the absolute gradient convergence criterion |
ABSXCONV=r <n> |
specifies the absolute change parameter convergence criterion |
FCONV=r <n> |
specifies the relative change function convergence criterion |
FCONV2=r <n> |
specifies the function convergence criterion |
FDIGITS=r |
specifies the precision in computation of the objective function |
FSIZE=r |
specifies the parameter for FCONV= and GCONV= |
GCONV=r <n> |
specifies the relative gradient convergence criterion |
GCONV2=r <n> |
specifies the relative gradient convergence criterion |
XCONV=r <n> |
specifies the relative change parameter convergence criterion |
XSIZE=r |
specifies the parameter for XCONV= |
Options for Nonlinearly Constrained Techniques |
|
ABSGCONV=r <n> |
specifies the maximum absolute gradient of Lagrange function criterion |
FCONV2=r <n> |
specifies the predicted objective function reduction criterion |
GCONV=r <n> |
specifies the normalized predicted objective function reduction criterion |
Option |
Description |
|---|---|
Options for the Approximate Covariance Matrix of Parameter Estimates |
|
CFACTOR=r |
specifies the scalar factor for standard errors |
NOHLF |
uses the Hessian of the objective function for standard errors |
Options for Additional Displayed Output |
|
PALL |
displays the initial and final optimization values |
PCRPJAC |
displays the approximate Hessian matrix |
PHESSIAN |
displays the Hessian matrix |
PHISTORY |
displays the optimization history |
PINIT |
displays the initial values and derivatives |
PNLCJAC |
displays the Jacobian matrix of nonlinear constraints |
displays the results of the optimization process |
|
Additional Options for Optimization Techniques |
|
DAMPSTEP< =r > |
controls the initial line-search step size |
HESCAL=n |
specifies the scaling version of Hessian or Jacobian |
LCDEACT=r |
specifies the Lagrange multiplier threshold of constraint |
LCEPSILON=r |
specifies the range for boundary and linear constraints |
LCSINGULAR=r |
specifies the QR decomposition linear dependence criterion |
NOEIGNUM |
suppresses the computation of matrices |
RESTART=i |
specifies the restart algorithm with a steepest descent direction |
VERSION=1 | 2 |
specifies the quasi-Newton optimization technique version |
Options Documented in the PROC CALIS Statement
The following options are the same as in the PROC CALIS statement and are documented in the section PROC CALIS Statement.
Estimation Method Option
Optimization Technique Options
- FCONV | FTOL=r
specifies the relative function convergence criterion. For more details, see the section Termination Criteria Options.
- GCONV | GTOL=r
specifies the relative gradient convergence criterion. For more details, see the section Termination Criteria Options.
- INSTEP | SALPHA | RADIUS=r
restricts the step length of an optimization algorithm during the first iterations.
- LINESEARCH | LIS=i
specifies the line-search method for the CONGRA, QUANEW, and NEWRAP optimization techniques.
- LSPRECISION | LSP=r
specifies the degree of accuracy that should be obtained by the line-search algorithms LIS=2 and LIS=3.
- MAXFUNC | MAXFU=i
specifies the maximum number
 of function calls in the optimization process. For more details, see the section Termination Criteria Options.
of function calls in the optimization process. For more details, see the section Termination Criteria Options. - MAXITER | MAXIT=i <n>
specifies the maximum number
 of iterations in the optimization process. For more details, see the section Termination Criteria Options.
of iterations in the optimization process. For more details, see the section Termination Criteria Options. - TECHNIQUE | TECH=name
- OMETHOD | OM=name
- UPDATE | UPD=name
specifies the update method for the quasi-Newton or conjugate-gradient optimization technique.
Miscellaneous Options
- ASINGULAR | ASING=r
specifies an absolute singularity criterion
 ,
, 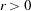 , for the inversion of the information matrix, which is needed to compute the approximate covariance matrix of parameter estimates.
, for the inversion of the information matrix, which is needed to compute the approximate covariance matrix of parameter estimates. - COVSING=r
specifies a nonnegative threshold
 ,
, 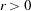 , that decides whether the eigenvalues of the information matrix are considered to be zero. This option is valid only for applications where the approximate covariance matrix of parameter estimates is found to be singular.
, that decides whether the eigenvalues of the information matrix are considered to be zero. This option is valid only for applications where the approximate covariance matrix of parameter estimates is found to be singular. - MSINGULAR | MSING=r
specifies a relative singularity criterion
 ,
, 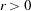 , for the inversion of the information matrix, which is needed to compute the approximate covariance matrix of parameter estimates.
, for the inversion of the information matrix, which is needed to compute the approximate covariance matrix of parameter estimates. - SINGULAR | SING =r
specifies the singularity criterion
 ,
,  , that is used for the inversion of the Hessian matrix. The default value is 1E
, that is used for the inversion of the Hessian matrix. The default value is 1E 8.
8. - VSINGULAR | VSING=r
specifies a relative singularity criterion
 ,
, 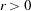 , for the inversion of the information matrix, which is needed to compute the approximate covariance matrix of parameter estimates.
, for the inversion of the information matrix, which is needed to compute the approximate covariance matrix of parameter estimates.
Termination Criteria Options
Let 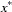 be the point at which the objective function
be the point at which the objective function 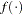 is optimized, and let
is optimized, and let 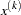 be the parameter values attained at the
be the parameter values attained at the 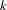 th iteration. All optimization techniques stop at the
th iteration. All optimization techniques stop at the 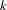 th iteration if at least one of a set of termination criteria is satisfied. The specified termination criteria should enable termination in an area of sufficient size around
th iteration if at least one of a set of termination criteria is satisfied. The specified termination criteria should enable termination in an area of sufficient size around 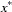 . You can avoid termination respective to any of the following function, gradient, or parameter criteria by setting the corresponding option to zero. There is a default set of termination criteria for each optimization technique; most of these default settings make the criteria ineffective for termination. PROC CALIS might have problems due to rounding errors (especially in derivative evaluations) that prevent an optimizer from satisfying strong termination criteria.
. You can avoid termination respective to any of the following function, gradient, or parameter criteria by setting the corresponding option to zero. There is a default set of termination criteria for each optimization technique; most of these default settings make the criteria ineffective for termination. PROC CALIS might have problems due to rounding errors (especially in derivative evaluations) that prevent an optimizer from satisfying strong termination criteria.
Note that PROC CALIS also terminates if the point 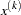 is fully constrained by linearly independent active linear or boundary constraints, and all Lagrange multiplier estimates of active inequality constraints are greater than a small negative tolerance.
is fully constrained by linearly independent active linear or boundary constraints, and all Lagrange multiplier estimates of active inequality constraints are greater than a small negative tolerance.
The following options are available only in the NLOPTIONS statement (except for FCONV, GCONV, MAXFUNC, and MAXITER), and they affect the termination criteria.
Options Used by All Optimization Techniques
- ABSCONV | ABSTOL=r
specifies an absolute function convergence criterion.
For minimization, termination requires
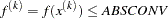
For maximization, termination requires
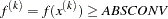
The default value of ABSCONV is as follows:
for minimization, the negative square root of the largest double-precision value
for maximization, the positive square root of the largest double-precision value
- MAXFUNC | MAXFU=i
requires the number of function calls to be no larger than
 . The default values are listed in the following table.
. The default values are listed in the following table. TECH=
MAXFUNC Default
LEVMAR, NEWRAP, NRRIDG, TRUREG
 =125
=125 DBLDOG, QUANEW
 =500
=500 CONGRA
 =1000
=1000 The default is used if you specify MAXFUNC=0. The optimization can be terminated only after completing a full iteration. Therefore, the number of function calls that are actually performed can exceed the number that is specified by the MAXFUNC= option.
- MAXITER | MAXIT= i <n>
requires the number of iterations to be no larger than
 . The default values are listed in the following table.
. The default values are listed in the following table. TECH=
MAXITER Default
LEVMAR, NEWRAP, NRRIDG, TRUREG
 =50
=50 DBLDOG, QUANEW
 =200
=200 CONGRA
 =400
=400 The default is used if you specify MAXITER=0 or you omit the MAXITER option.
The optional second value
 is valid only for TECH=QUANEW with nonlinear constraints. It specifies an upper bound
is valid only for TECH=QUANEW with nonlinear constraints. It specifies an upper bound  for the number of iterations of an algorithm and reduces the violation of nonlinear constraints at a starting point. The default value is
for the number of iterations of an algorithm and reduces the violation of nonlinear constraints at a starting point. The default value is  =20. For example, specifying MAXITER= . 0 means that you do not want to exceed the default number of iterations during the main optimization process and that you want to suppress the feasible-point algorithm for nonlinear constraints.
=20. For example, specifying MAXITER= . 0 means that you do not want to exceed the default number of iterations during the main optimization process and that you want to suppress the feasible-point algorithm for nonlinear constraints. - MAXTIME=r
requires the CPU time to be no larger than
 . The default value of the MAXTIME= option is the largest double floating-point number on your computer.
. The default value of the MAXTIME= option is the largest double floating-point number on your computer. - MINITER | MINIT=i
specifies the minimum number of iterations. The default value is
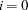 .
. The ABSCONV=, MAXITER=, MAXFUNC=, and MAXTIME= options are useful for dividing a time-consuming optimization problem into a series of smaller problems by using the OUTEST= and INEST= data sets.
Options for Unconstrained and Linearly Constrained Optimization Techniques
- ABSFCONV | ABSFTOL=r <n>
specifies the absolute function convergence criterion. Termination requires a small change of the function value in successive iterations,
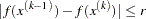
The default value is
 . The optional integer value
. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. - ABSGCONV | ABSGTOL=r <n>
specifies the absolute gradient convergence criterion. Termination requires the maximum absolute gradient element to be small,
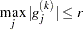
The default value is
 =1E
=1E 5. The optional integer value
5. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. Note:In some applications, the small default value of the ABSGCONV= criterion is too difficult to satisfy for some of the optimization techniques.
- ABSXCONV | ABSXTOL=r <n>
specifies the absolute parameter convergence criterion. Termination requires a small Euclidean distance between successive parameter vectors,
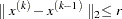
The default value is
 . The optional integer value
. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. - FCONV | FTOL=r <n>
specifies the relative function convergence criterion. Termination requires a small relative change of the function value in successive iterations,
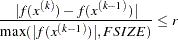
where
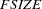 is defined by the FSIZE= option. The default value is
is defined by the FSIZE= option. The default value is 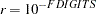 , where
, where 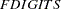 either is specified or is set by default to
either is specified or is set by default to 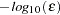 , where
, where  is the machine precision. The optional integer value
is the machine precision. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. - FCONV2 | FTOL2=r <n>
specifies another function convergence criterion. For least squares problems, termination requires a small predicted reduction
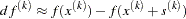
of the objective function.
The predicted reduction





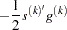



is computed by approximating the objective function
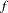 by the first two terms of the Taylor series and substituting the Newton step
by the first two terms of the Taylor series and substituting the Newton step 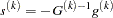
The FCONV2 criterion is the unscaled version of the GCONV criterion. The default value is
 . The optional integer value
. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. - FDIGITS=r
specifies the number of accurate digits in evaluations of the objective function. Fractional values such as FDIGITS=4.7 are allowed. The default value is
 , where
, where  is the machine precision. The value of
is the machine precision. The value of  is used for the specification of the default value of the FCONV= option.
is used for the specification of the default value of the FCONV= option. - FSIZE=r
specifies the
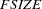 parameter of the relative function and relative gradient termination criteria. The default value is
parameter of the relative function and relative gradient termination criteria. The default value is  . See the FCONV= and GCONV= options for details.
. See the FCONV= and GCONV= options for details. - GCONV | GTOL=r <n>
specifies the relative gradient convergence criterion. For all techniques except the CONGRA technique, termination requires that the normalized predicted function reduction be small,

where
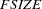 is defined by the FSIZE= option. For the CONGRA technique (where a reliable Hessian estimate
is defined by the FSIZE= option. For the CONGRA technique (where a reliable Hessian estimate  is not available),
is not available), 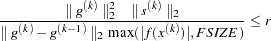
is used. The default value is
 =1E
=1E 8. The optional integer value
8. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. Note:The default setting for the GCONV= option sometimes leads to early termination far from the location of the optimum. This is especially true for the special form of this criterion used in the CONGRA optimization.
- GCONV2 | GTOL2=r <n>
specifies another relative gradient convergence criterion. For least squares problems and the TRUREG, LEVMAR, NRRIDG, and NEWRAP techniques, the criterion of Browne (1982) is used,

This criterion is not used by the other techniques. The default value is
 . The optional integer value
. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. - XCONV | XTOL=r <n>
specifies the relative parameter convergence criterion. Termination requires a small relative parameter change in subsequent iterations,

The default value is
 . The optional integer value
. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. - XSIZE=r
specifies the
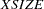 parameter of the relative function and relative gradient termination criteria. The default value is
parameter of the relative function and relative gradient termination criteria. The default value is  . See the XCONV= option for details.
. See the XCONV= option for details.
Options for Nonlinearly Constrained Techniques
The non-NMSIMP algorithms available for nonlinearly constrained optimization (currently only TECH=QUANEW) do not monotonically reduce either the value of the objective function or some kind of merit function that combines objective and constraint functions. Furthermore, the algorithm uses the watchdog technique with backtracking (Chamberlain et al., 1982). Therefore, no termination criteria are implemented that are based on the values ( or
or  ) of successive iterations. In addition to the criteria used by all optimization techniques, only three more termination criteria are currently available, and they are based on the Lagrange function:
) of successive iterations. In addition to the criteria used by all optimization techniques, only three more termination criteria are currently available, and they are based on the Lagrange function:
 |
and its gradient
 |
Here, 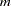 denotes the total number of constraints,
denotes the total number of constraints, 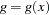 denotes the gradient of the objective function, and
denotes the gradient of the objective function, and 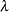 denotes the
denotes the 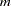 vector of Lagrange multipliers. The Kuhn-Tucker conditions require that the gradient of the Lagrange function is zero at the optimal point
vector of Lagrange multipliers. The Kuhn-Tucker conditions require that the gradient of the Lagrange function is zero at the optimal point  :
:
 |
The termination criteria available for nonlinearly constrained optimization follow.
- ABSGCONV | ABSGTOL=r <n>
specifies that termination requires the maximum absolute gradient element of the Lagrange function to be small,
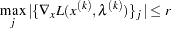
The default value is
 =1E
=1E 5. The optional integer value
5. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. - FCONV2 | FTOL2=r <n>
specifies that termination requires the predicted objective function reduction to be small:
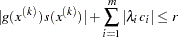
The default value is
 =1E
=1E 6. This is the criterion used by the programs VMCWD and VF02AD (Powell 1982b). The optional integer value
6. This is the criterion used by the programs VMCWD and VF02AD (Powell 1982b). The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated. - GCONV | GTOL=r <n>
specifies that termination requires the normalized predicted objective function reduction to be small:
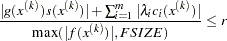
where
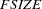 is defined by the FSIZE= option. The default value is
is defined by the FSIZE= option. The default value is  =1E
=1E 8. The optional integer value
8. The optional integer value  determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.
Miscellaneous Options
Options for the Approximate Covariance Matrix of Parameter Estimates
- CFACTOR=r
specifies the scalar factor for the covariance matrix of parameter estimates. The scalar
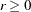 replaces the default value
replaces the default value  . For more details, see the section Approximate Standard Errors.
. For more details, see the section Approximate Standard Errors. - NOHLF
specifies that the Hessian matrix of the objective function (rather than the Hessian matrix of the Lagrange function) be used for computing the approximate covariance matrix of parameter estimates and, therefore, the approximate standard errors.
It is theoretically not correct to use the NOHLF option. However, since most implementations use the Hessian matrix of the objective function and not the Hessian matrix of the Lagrange function for computing approximate standard errors, the NOHLF option can be used to compare the results.
Options for Additional Displayed Output
- PALL | ALL
displays information about the starting values and final values of the optimization process.
- PCRPJAC | PJTJ
displays the approximate Hessian matrix. If general linear or nonlinear constraints are active at the solution, the projected approximate Hessian matrix is also displayed.
- PHESSIAN | PHES
displays the Hessian matrix. If general linear or nonlinear constraints are active at the solution, the projected Hessian matrix is also displayed.
- PHISTORY | PHIS
displays the optimization history. The PHISTORY option is set automatically if the PALL or PRINT option is set.
- PINIT | PIN
displays the initial values and derivatives (if available). The PINIT option is set automatically if the PALL option is set.
- PNLCJAC
displays the Jacobian matrix of nonlinear constraints specified by the NLINCON statement. The PNLCJAC option is set automatically if the PALL option is set.
- PRINT | PRI
displays the results of the optimization process, such as parameter estimates and constraints.
Options for Fine-Tuning Optimization Techniques
- DAMPSTEP | DS <=r>
specifies that the initial step-size value
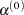 for each line search (used by the QUANEW, CONGRA, or NEWRAP technique) cannot be larger than
for each line search (used by the QUANEW, CONGRA, or NEWRAP technique) cannot be larger than  times the step-size value used in the former iteration. If the factor
times the step-size value used in the former iteration. If the factor  is not specified, the default value is
is not specified, the default value is 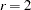 . The DAMPSTEP option can prevent the line-search algorithm from repeatedly stepping into regions where some objective functions are difficult to compute or where they can lead to floating-point overflows during the computation of objective functions and their derivatives. The DAMPSTEP<=
. The DAMPSTEP option can prevent the line-search algorithm from repeatedly stepping into regions where some objective functions are difficult to compute or where they can lead to floating-point overflows during the computation of objective functions and their derivatives. The DAMPSTEP<= > option can prevent time-costly function calls during line searches with very small step sizes
> option can prevent time-costly function calls during line searches with very small step sizes  of objective functions. For more information about setting the start values of each line search, see the section Restricting the Step Length.
of objective functions. For more information about setting the start values of each line search, see the section Restricting the Step Length. - HESCAL | HS = 0 | 1 | 2 | 3
specifies the scaling version of the Hessian or crossproduct Jacobian matrix used in NRRIDG, TRUREG, LEVMAR, NEWRAP, or DBLDOG optimization. If HS is not equal to zero, the first iteration and each restart iteration set the diagonal scaling matrix
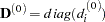 :
: 
where
 are the diagonal elements of the Hessian or crossproduct Jacobian matrix. In every other iteration, the diagonal scaling matrix
are the diagonal elements of the Hessian or crossproduct Jacobian matrix. In every other iteration, the diagonal scaling matrix 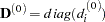 is updated depending on the HS option:
is updated depending on the HS option: - HS=0
specifies that no scaling is done.
- HS=1
specifies the Moré (1978) scaling update:
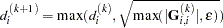
- HS=2
specifies the Dennis, Gay, and Welsch (1981) scaling update:
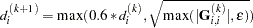
- HS=3
specifies that
 is reset in each iteration:
is reset in each iteration: 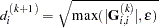
In the preceding equations,
 is the relative machine precision. The default is HS=1 for LEVMAR minimization and HS=0 otherwise. Scaling of the Hessian or crossproduct Jacobian can be time-consuming in the case where general linear constraints are active.
is the relative machine precision. The default is HS=1 for LEVMAR minimization and HS=0 otherwise. Scaling of the Hessian or crossproduct Jacobian can be time-consuming in the case where general linear constraints are active. - LCDEACT | LCD=r
specifies a threshold
 for the Lagrange multiplier that decides whether an active inequality constraint remains active or can be deactivated. For maximization,
for the Lagrange multiplier that decides whether an active inequality constraint remains active or can be deactivated. For maximization,  must be greater than zero; for minimization,
must be greater than zero; for minimization,  must be smaller than zero. The default is
must be smaller than zero. The default is 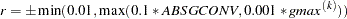
where "
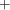 " stands for maximization, "
" stands for maximization, " " stands for minimization,
" stands for minimization, 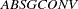 is the value of the absolute gradient criterion, and
is the value of the absolute gradient criterion, and 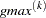 is the maximum absolute element of the (projected) gradient
is the maximum absolute element of the (projected) gradient  or
or  .
. - LCEPSILON | LCEPS | LCE=r
specifies the range
 ,
, 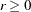 , for active and violated boundary and linear constraints. If the point
, for active and violated boundary and linear constraints. If the point 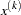 satisfies the condition
satisfies the condition 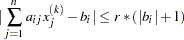
the constraint
 is recognized as an active constraint. Otherwise, the constraint
is recognized as an active constraint. Otherwise, the constraint  is either an inactive inequality or a violated inequality or equality constraint. The default value is
is either an inactive inequality or a violated inequality or equality constraint. The default value is  =1E
=1E 8. During the optimization process, the introduction of rounding errors can force PROC NLP to increase the value of
8. During the optimization process, the introduction of rounding errors can force PROC NLP to increase the value of  by factors of 10. If this happens, it is indicated by a message displayed in the log.
by factors of 10. If this happens, it is indicated by a message displayed in the log. - LCSINGULAR | LCSING | LCS=r
specifies a criterion
 ,
, 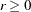 , used in the update of the QR decomposition that decides whether an active constraint is linearly dependent on a set of other active constraints. The default is
, used in the update of the QR decomposition that decides whether an active constraint is linearly dependent on a set of other active constraints. The default is  =1E
=1E 8. The larger
8. The larger  becomes, the more the active constraints are recognized as being linearly dependent.
becomes, the more the active constraints are recognized as being linearly dependent. - NOEIGNUM
suppresses the computation and displayed output of the determinant and the inertia of the Hessian, crossproduct Jacobian, and covariance matrices. The inertia of a symmetric matrix are the numbers of negative, positive, and zero eigenvalues. For large applications, the NOEIGNUM option can save computer time.
- RESTART | REST=i
specifies that the QUANEW or CONGRA algorithm is restarted with a steepest descent/ascent search direction after at most
 iterations,
iterations, 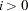 . Default values are as follows:
. Default values are as follows: CONGRA: UPDATE=PB: restart is done automatically so specification of
 is not used.
is not used. CONGRA: UPDATE
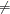 PB:
PB: 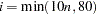 , where
, where  is the number of parameters.
is the number of parameters. QUANEW:
 is the largest integer available.
is the largest integer available.
- VERSION | VS = 1 | 2
specifies the version of the quasi-Newton optimization technique with nonlinear constraints.
- VS=1
specifies the update of the
 vector as in Powell (1978a, 1978b) (update like VF02AD).
vector as in Powell (1978a, 1978b) (update like VF02AD). - VS=2
specifies the update of the
 vector as in Powell (1982a, 1982b) (update like VMCWD).
vector as in Powell (1982a, 1982b) (update like VMCWD).
The default is VS=2.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.