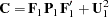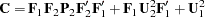| The CALIS Procedure |
| Structural Equation Models |
The Generalized COSAN Model
PROC CALIS can analyze matrix models of the form
 |
where 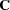 is a symmetric correlation or covariance matrix, each matrix
is a symmetric correlation or covariance matrix, each matrix 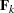 ,
,  is the product of
is the product of 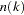 matrices
matrices 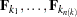 , and each matrix
, and each matrix 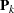 is symmetric; that is,
is symmetric; that is,
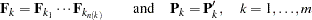 |
The matrices 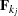 and
and 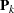 in the model are parameterized by the matrices
in the model are parameterized by the matrices  and
and 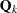
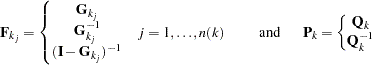 |
where you can specify the type of matrix desired.
The matrices  and
and 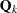 can contain the following:
can contain the following:
constant values
parameters to be estimated
values computed from parameters via programming statements
The parameters can be summarized in a parameter vector 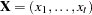 . For a given covariance or correlation matrix
. For a given covariance or correlation matrix 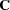 , PROC CALIS computes the unweighted least squares (ULS), generalized least squares (GLS), maximum likelihood (ML), weighted least squares (WLS), or diagonally weighted least squares (DWLS) estimates of the vector
, PROC CALIS computes the unweighted least squares (ULS), generalized least squares (GLS), maximum likelihood (ML), weighted least squares (WLS), or diagonally weighted least squares (DWLS) estimates of the vector  .
.
Some Special Cases of the Generalized COSAN Model
Reticular Action Model—RAM (McArdle 1980; McArdle and McDonald 1984)
Structural equation model:
 |
where 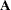 is a matrix of coefficients, and
is a matrix of coefficients, and  and
and  are vectors of random variables. The variables in
are vectors of random variables. The variables in  and
and  can be manifest or latent variables. The endogenous variables corresponding to the components in
can be manifest or latent variables. The endogenous variables corresponding to the components in  are expressed as a linear combination of the remaining variables and a residual component in
are expressed as a linear combination of the remaining variables and a residual component in  with covariance matrix
with covariance matrix 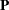 .
.
Covariance structure:
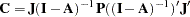 |
with selection matrix 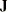 and
and
 |
LINEQS (Linear Equations) Model (Bentler and Weeks 1980)
Structural equation model:
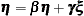 |
where 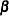 and
and  are coefficient matrices, and
are coefficient matrices, and 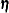 and
and  are vectors of random variables. The components of
are vectors of random variables. The components of 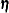 correspond to the endogenous variables; the components of
correspond to the endogenous variables; the components of  correspond to the exogenous variables and to error variables. The variables in
correspond to the exogenous variables and to error variables. The variables in 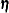 and
and  can be manifest or latent variables. The endogenous variables in
can be manifest or latent variables. The endogenous variables in 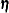 are expressed as a linear combination of the remaining endogenous variables, the exogenous variables in
are expressed as a linear combination of the remaining endogenous variables, the exogenous variables in  , and a residual component in
, and a residual component in  . The coefficient matrix
. The coefficient matrix 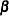 describes the relationships among the endogenous variables of
describes the relationships among the endogenous variables of 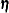 , and
, and 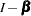 should be nonsingular. The coefficient matrix
should be nonsingular. The coefficient matrix  describes the relationships between the endogenous variables of
describes the relationships between the endogenous variables of 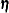 and the exogenous and error variables of
and the exogenous and error variables of  .
.
Covariance structure:
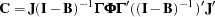 |
with selection matrix 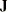 ,
, 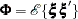 , and
, and
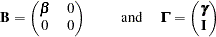 |
Keesling-Wiley-Jöreskog LISREL (Linear Structural Relationship) Model (Keesling 1972; Wiley 1973; Jöreskog 1973)
Structural equation model and measurement models:
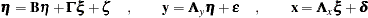 |
where 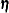 and
and  are vectors of latent variables (factors), and
are vectors of latent variables (factors), and  and
and 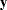 are vectors of manifest variables. The components of
are vectors of manifest variables. The components of 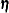 correspond to endogenous latent variables; the components of
correspond to endogenous latent variables; the components of  correspond to exogenous latent variables. The endogenous and exogenous latent variables are connected by a system of linear equations (the structural model) with coefficient matrices
correspond to exogenous latent variables. The endogenous and exogenous latent variables are connected by a system of linear equations (the structural model) with coefficient matrices  and
and  and an error vector
and an error vector 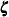 . It is assumed that matrix
. It is assumed that matrix  is nonsingular. The random vectors
is nonsingular. The random vectors 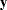 and
and  correspond to manifest variables that are related to the latent variables
correspond to manifest variables that are related to the latent variables 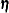 and
and  by two systems of linear equations (the measurement model) with coefficients
by two systems of linear equations (the measurement model) with coefficients 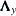 and
and 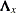 and with measurement errors
and with measurement errors  and
and 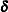 .
.
Covariance structure:
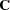 |
 |
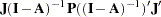 |
|||
 |
 |
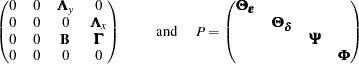 |
with selection matrix 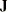 ,
, 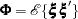 ,
,  ,
, 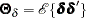 , and
, and  .
.
First-Order Autoregressive Longitudinal Factor Model
Example of McDonald (1980):  : Occasions of Measurement;
: Occasions of Measurement; 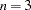 : Variables (Tests);
: Variables (Tests); 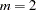 : Common Factors
: Common Factors
 |
 |
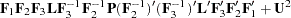 |
|||
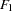 |
 |
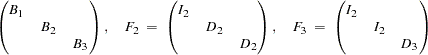 |
|||
 |
 |
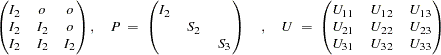 |
|||
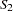 |
 |
 |
For more information about this model, see Example 25.6.
A Structural Equation Example
This example from Wheaton et al. (1977) illustrates the relationships among the RAM, LINEQS, and LISREL models. Different structural models for these data are in Jöreskog and Sörbom (1985) and in Bentler (1985, p. 28). The data set contains covariances among six (manifest) variables collected from 932 people in rural regions of Illinois:
- Variable 1:
V1,
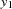 : Anomie 1967
: Anomie 1967 - Variable 2:
V2,
 : Powerlessness 1967
: Powerlessness 1967 - Variable 3:
V3,
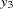 : Anomie 1971
: Anomie 1971 - Variable 4:
V4,
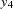 : Powerlessness 1971
: Powerlessness 1971 - Variable 5:
V5,
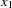 : Education (years of schooling)
: Education (years of schooling) - Variable 6:
V6,
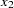 : Duncan’s Socioeconomic Index (SEI)
: Duncan’s Socioeconomic Index (SEI)
It is assumed that anomie and powerlessness are indicators of an alienation factor and that education and SEI are indicators for a socioeconomic status (SES) factor. Hence, the analysis contains three latent variables:
- Variable 7:
F1,
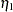 : Alienation 1967
: Alienation 1967 - Variable 8:
F2,
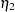 : Alienation 1971
: Alienation 1971 - Variable 9:
F3,
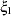 : Socioeconomic Status (SES)
: Socioeconomic Status (SES)
The following path diagram shows the structural model used in Bentler (1985, p. 29) and slightly modified in Jöreskog and Sörbom (1985, p. 56). In this notation for the path diagram, regression coefficients between the variables are indicated as one-headed arrows. Variances and covariances among the variables are indicated as two-headed arrows. Indicating error variances and covariances as two-headed arrows with the same source and destination (McArdle 1988; McDonald 1985) is helpful in transforming the path diagram to RAM model list input for the CALIS procedure.
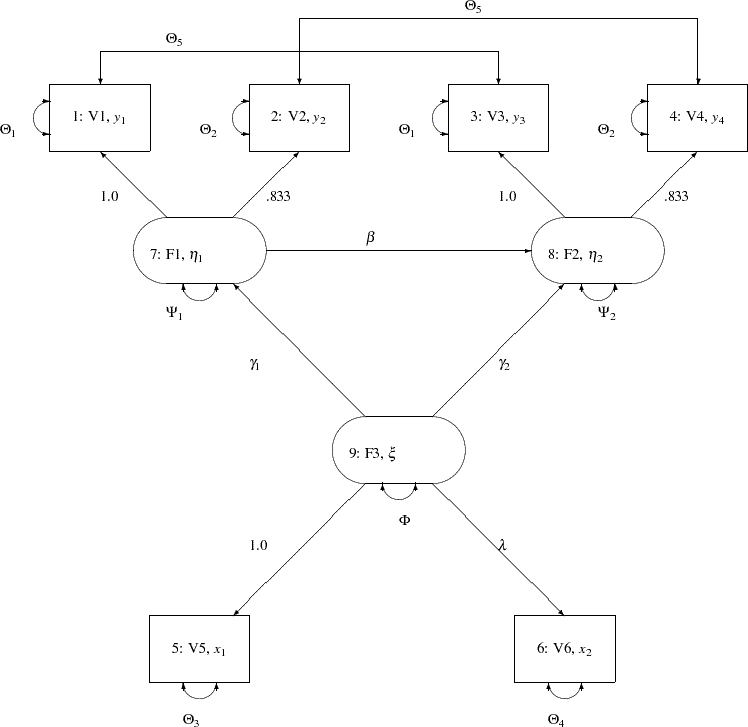
Variables in Figure 25.1 are as follows:
- Variable 1:
V1,
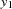 : Anomie 1967
: Anomie 1967 - Variable 2:
V2,
 : Powerlessness 1967
: Powerlessness 1967 - Variable 3:
V3,
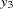 : Anomie 1971
: Anomie 1971 - Variable 4:
V4,
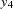 : Powerlessness 1971
: Powerlessness 1971 - Variable 5:
V5,
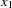 : Education (years of schooling)
: Education (years of schooling) - Variable 6:
V6,
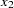 : Duncan’s Socioeconomic Index (SEI)
: Duncan’s Socioeconomic Index (SEI) - Variable 7:
F1,
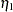 : Alienation 1967
: Alienation 1967 - Variable 8:
F2,
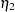 : Alienation 1971
: Alienation 1971 - Variable 9:
F3,
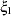 : Socioeconomic Status (SES)
: Socioeconomic Status (SES)
LINEQS Model
The vector 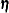 contains the six endogenous manifest variables V1, ..., V6 and the two endogenous latent variables F1 and F2. The vector
contains the six endogenous manifest variables V1, ..., V6 and the two endogenous latent variables F1 and F2. The vector  contains the exogenous error variables E1, ..., E6, D1, and D2 and the exogenous latent variable F3. The path diagram corresponds to the following set of structural equations of the LINEQS model:
contains the exogenous error variables E1, ..., E6, D1, and D2 and the exogenous latent variable F3. The path diagram corresponds to the following set of structural equations of the LINEQS model:
 |
 |
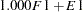 |
|||
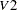 |
 |
 |
|||
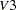 |
 |
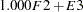 |
|||
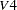 |
 |
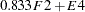 |
|||
 |
 |
 |
|||
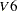 |
 |
 |
|||
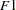 |
 |
 |
|||
 |
 |
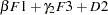 |
This gives the matrices 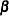 ,
,  , and
, and 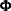 in the LINEQS model:
in the LINEQS model:
 |
 |
The LINEQS model input specification of this example for the CALIS procedure is given in the section LINEQS Model Specification.
RAM Model
The vector  contains the six manifest variables
contains the six manifest variables 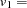 V1, ...,
V1, ..., 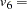 V6 and the three latent variables
V6 and the three latent variables 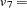 F1,
F1, 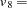 F2,
F2, 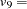 F3. The vector
F3. The vector  contains the corresponding error variables
contains the corresponding error variables 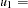 E1, ...,
E1, ...,  E6 and
E6 and  D1,
D1, 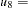 D2,
D2,  D3. The path diagram corresponds to the following set of structural equations of the RAM model:
D3. The path diagram corresponds to the following set of structural equations of the RAM model:
 |
 |
 |
|||
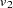 |
 |
 |
|||
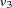 |
 |
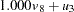 |
|||
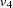 |
 |
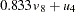 |
|||
 |
 |
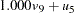 |
|||
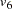 |
 |
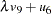 |
|||
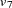 |
 |
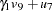 |
|||
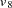 |
 |
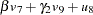 |
|||
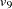 |
 |
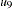 |
This gives the matrices 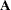 and
and 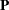 in the RAM model:
in the RAM model:
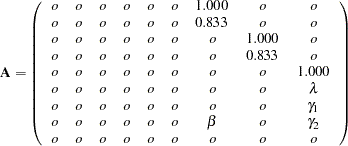 |
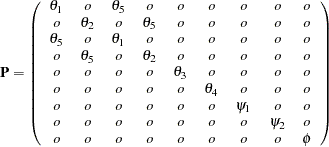 |
The RAM model input specification of this example for the CALIS procedure is given in the section RAM Model Specification.
LISREL Model
The vector 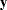 contains the four endogenous manifest variables
contains the four endogenous manifest variables 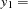 V1, ...,
V1, ..., 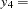 V4, and the vector
V4, and the vector  contains the exogenous manifest variables
contains the exogenous manifest variables 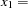 V5 and
V5 and 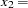 V6. The vector
V6. The vector  contains the error variables
contains the error variables  E1, ...,
E1, ..., 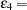 E4 corresponding to
E4 corresponding to 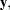 and the vector
and the vector 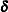 contains the error variables
contains the error variables 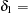 E5 and
E5 and  E6 corresponding to
E6 corresponding to  . The vector
. The vector 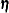 contains the endogenous latent variables (factors)
contains the endogenous latent variables (factors)  F1 and
F1 and 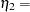 F2, while the vector
F2, while the vector  contains the exogenous latent variable (factor)
contains the exogenous latent variable (factor) 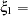 F3. The vector
F3. The vector 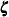 contains the errors
contains the errors 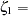 D1 and
D1 and  D2 in the equations (disturbance terms) corresponding to
D2 in the equations (disturbance terms) corresponding to 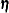 . The path diagram corresponds to the following set of structural equations of the LISREL model:
. The path diagram corresponds to the following set of structural equations of the LISREL model:
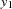 |
 |
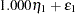 |
|||
 |
 |
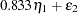 |
|||
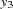 |
 |
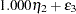 |
|||
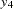 |
 |
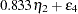 |
|||
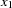 |
 |
 |
|||
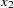 |
 |
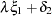 |
|||
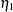 |
 |
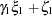 |
|||
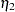 |
 |
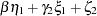 |
This gives the matrices 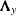 ,
,  ,
,  ,
,  , and
, and 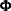 in the LISREL model:
in the LISREL model:
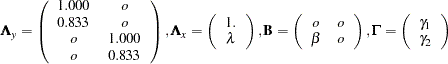 |
 |
The CALIS procedure does not provide a LISREL model input specification. However, any model that can be specified by the LISREL model can also be specified by using the LINEQS, RAM, or COSAN model specifications in PROC CALIS.
Copyright © 2009 by SAS Institute Inc., Cary, NC, USA. All rights reserved.