specifies the level of significance for comparisons among the means. By default, ALPHA=0.05. You can specify any value greater than 0 and less than 1.

performs Bonferroni tests of differences between means for all main effect means in the MEANS statement. See the CLDIFF and LINES options, which follow, for a discussion of how the procedure displays results.

presents results of the BON, GABRIEL, SCHEFFE, SIDAK,SMM, GT2, T, LSD, and TUKEY options as confidence intervals for all pairwise differences between means, and the results of the DUNNETT, DUNNETTU, and DUNNETTL options as confidence intervals for differences with the control. The CLDIFF option is the default for unequal cell sizes unless the DUNCAN, REGWQ, SNK, or WALLER option is specified.

presents results of the BON, GABRIEL, SCHEFFE, SIDAK,SMM, T, and LSD options as intervals for the mean of each level of the variables specified in the MEANS statement. For all options except GABRIEL, the intervals are confidence intervals for the true means. For the GABRIEL option, they are comparison intervals for comparing means pairwise: in this case, if the intervals corresponding to two means overlap, the difference between them is insignificant according to Gabriel’s method.

performs Duncan’s multiple range test on all main effect means given in the MEANS statement. See the LINES option for a discussion of how the procedure displays results.

performs Dunnett’s two-tailed test, testing if any treatments are significantly different from a single control for all main effects means in the MEANS statement.

To specify which level of the effect is the control, enclose the formatted value in quotes in parentheses after the keyword. If more than one effect is specified in the MEANS statement, you can use a list of control values within the parentheses. By default, the first level of the effect is used as the control. For example,

   means a / dunnett('CONTROL');

where CONTROL is the formatted control value of A. As another example,

   means a b c / dunnett('CNTLA' 'CNTLB' 'CNTLC');

where CNTLA, CNTLB, and CNTLC are the formatted control values for A, B, and C, respectively.

performs Dunnett’s one-tailed test, testing if any treatment is significantly less than the control. Control level information is specified as described previously for the DUNNETT option.

performs Dunnett’s one-tailed test, testing if any treatment is significantly greater than the control. Control level information is specified as described previously for the DUNNETT option.

specifies the error mean square used in the multiple comparisons. By default, PROC ANOVA uses the residual Mean Square (MS). The effect specified with the E= option must be a term in the model; otherwise, the procedure uses the residual MS.

performs Gabriel’s multiple-comparison procedure on all main effect means in the MEANS statement. See the CLDIFF and LINES options for discussions of how the procedure displays results.

see the SMM option.

requests a homogeneity of variance test for the groups defined by the MEANS effect. You can optionally specify a particular test; if you do not specify a test, Levene’s test (Levene; 1960) with TYPE=SQUARE is computed. Note that this option is ignored unless your MODEL statement specifies a simple one-way model.

The HOVTEST=BARTLETT option specifies Bartlett’s test (Bartlett; 1937), a modification of the normal-theory likelihood ratio test.

The HOVTEST=BF option specifies Brown and Forsythe’s variation of Levene’s test (Brown and Forsythe; 1974).

The HOVTEST=LEVENE option specifies Levene’s test (Levene; 1960), which is widely considered to be the standard homogeneity of variance test. You can use the TYPE= option in parentheses to specify whether to use the absolute residuals (TYPE=ABS) or the squared residuals (TYPE=SQUARE) in Levene’s test. The default is TYPE=SQUARE.

The HOVTEST=OBRIEN option specifies O’Brien’s test (O’Brien; 1979), which is basically a modification of HOVTEST=LEVENE(TYPE=SQUARE). You can use the W= option in parentheses to tune the variable to match the suspected kurtosis of the underlying distribution. By default, W=0.5, as suggested by O’Brien (1979, 1981).

See the section Homogeneity of Variance in One-Way Models in Chapter 39, The GLM Procedure, for more details on these methods. Example 39.10 in the same chapter illustrates the use of the HOVTEST and WELCH options in the MEANS statement in testing for equal group variances.

specifies the Type 1/Type 2 error seriousness ratio for the Waller-Duncan test. Reasonable values for KRATIO are 50, 100, and 500, which roughly correspond for the two-level case to ALPHA levels of 0.1, 0.05, and 0.01. By default, the procedure uses the default value of 100.

presents results of the BON, DUNCAN, GABRIEL, REGWQ, SCHEFFE, SIDAK,SMM, GT2, SNK, T, LSD TUKEY, and WALLER options by listing the means in descending order and indicating nonsignificant subsets by line segments beside the corresponding means. The LINES option is appropriate for equal cell sizes, for which it is the default. The LINES option is also the default if the DUNCAN, REGWQ, SNK, or WALLER option is specified, or if there are only two cells of unequal size. If the cell sizes are unequal, the harmonic mean of the cell sizes is used, which might lead to somewhat liberal tests if the cell sizes are highly disparate. The LINES option cannot be used in combination with the DUNNETT, DUNNETTL, or DUNNETTU option. In addition, the procedure has a restriction that no more than 24 overlapping groups of means can exist. If a mean belongs to more than 24 groups, the procedure issues an error message. You can either reduce the number of levels of the variable or use a multiple comparison test that allows the CLDIFF option rather than the LINES option.

see the T option.

prevents the means from being sorted into descending order when the CLDIFF or CLM option is specified.

performs the Ryan-Einot-Gabriel-Welsch multiple range test on all main effect means in the MEANS statement. See the LINES option for a discussion of how the procedure displays results.

performs Scheffé’s multiple-comparison procedure on all main effect means in the MEANS statement. See the CLDIFF and LINES options for discussions of how the procedure displays results.

performs pairwise tests on differences between means with levels adjusted according to Sidak’s inequality for all main effect means in the MEANS statement. See the CLDIFF and LINES options for discussions of how the procedure displays results.

performs pairwise comparisons based on the studentized maximum modulus and Sidak’s uncorrelated- inequality, yielding Hochberg’s GT2 method when sample sizes are unequal, for all main effect means in the MEANS statement. See the CLDIFF and LINES options for discussions of how the procedure displays results.

performs the Student-Newman-Keuls multiple range test on all main effect means in the MEANS statement. See the LINES option for a discussion of how the procedure displays results.

performs pairwise tests, equivalent to Fisher’s least-significant-difference test in the case of equal cell sizes, for all main effect means in the MEANS statement. See the CLDIFF and LINES options for discussions of how the procedure displays results.

performs Tukey’s studentized range test (HSD) on all main effect means in the MEANS statement. (When the group sizes are different, this is the Tukey-Kramer test.) See the CLDIFF and LINES options for discussions of how the procedure displays results.

performs the Waller-Duncan 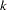-ratio test on all main effect means in the MEANS statement. See the KRATIO= option for information about controlling details of the test, and see the LINES option for a discussion of how the procedure displays results.

requests Welch’s (1951) variance-weighted one-way ANOVA. This alternative to the usual analysis of variance for a one-way model is robust to the assumption of equal within-group variances. This option is ignored unless your MODEL statement specifies a simple one-way model.

Note that using the WELCH option merely produces one additional table consisting of Welch’s ANOVA. It does not affect all of the other tests displayed by the ANOVA procedure, which still require the assumption of equal variance for exact validity.

See the section Homogeneity of Variance in One-Way Models in Chapter 39, The GLM Procedure, for more details on Welch’s ANOVA. Example 39.10 in the same chapter illustrates the use of the HOVTEST and WELCH options in the MEANS statement in testing for equal group variances.