The HPPLS Procedure
Reduced Rank Regression
As discussed in the preceding sections, partial least squares depends on selecting factors 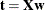 of the predictors and
of the predictors and 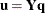 of the responses that have maximum covariance, whereas principal components regression effectively ignores
of the responses that have maximum covariance, whereas principal components regression effectively ignores  and selects
and selects 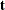 to have maximum variance, subject to orthogonality constraints. In contrast, reduced rank regression selects
to have maximum variance, subject to orthogonality constraints. In contrast, reduced rank regression selects  to account for as much variation in the predicted responses as possible, effectively ignoring the predictors for the purposes of factor extraction. In reduced rank regression,
the Y-weights
to account for as much variation in the predicted responses as possible, effectively ignoring the predictors for the purposes of factor extraction. In reduced rank regression,
the Y-weights 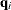 are the eigenvectors of the covariance matrix
are the eigenvectors of the covariance matrix 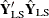 of the responses that are predicted by ordinary least squares regression, and the X-scores are the projections of the Y-scores
of the responses that are predicted by ordinary least squares regression, and the X-scores are the projections of the Y-scores
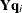 onto the X space.
onto the X space.
