The HPPLS Procedure

When you develop a predictive model, it is important to consider not only the explanatory power of the model for current responses, but also how well sampled the predictive functions are, because the sampling affects how well the model can extrapolate to future observations. All the techniques that the HPPLS procedure implements work by extracting successive factors (linear combinations of the predictors) that optimally address one or both of these two goals: explaining response variation and explaining predictor variation. In particular, principal components regression selects factors that explain as much predictor variation as possible, reduced rank regression selects factors that explain as much response variation as possible, and partial least squares balances the two objectives, seeking factors that explain both response and predictor variation.

To see the relationships between these methods, consider how each one extracts a single factor from the following artificial data set, which consists of two predictors and one response:

data data;
   input x1 x2 y;
   datalines;
    3.37651  2.30716        0.75615
    0.74193 -0.88845        1.15285
    4.18747  2.17373        1.42392
    0.96097  0.57301        0.27433
   -1.11161 -0.75225       -0.25410
   -1.38029 -1.31343       -0.04728
    1.28153 -0.13751        1.00341
   -1.39242 -2.03615        0.45518
    0.63741  0.06183        0.40699
   -2.52533 -1.23726       -0.91080
    2.44277  3.61077       -0.82590
;

proc hppls data=data nfac=1 method=rrr;
   model y = x1 x2;
run;

proc hppls data=data nfac=1 method=pcr;
   model y = x1 x2;
run;

proc hppls data=data nfac=1 method=pls;
   model y = x1 x2;
run;

The amount of model and response variation that are explained by the first factor for each method is shown in Figure 11.11 through Figure 11.13.

Notice that although the first reduced rank regression factor explains all of the response variation, it accounts for only about 15% of the predictor variation. In contrast, the first principal component regression factor accounts for most of the predictor variation (93%) but only 9% of the response variation. The first partial least squares factor accounts for only slightly less predictor variation than principal components but about three times as much response variation.

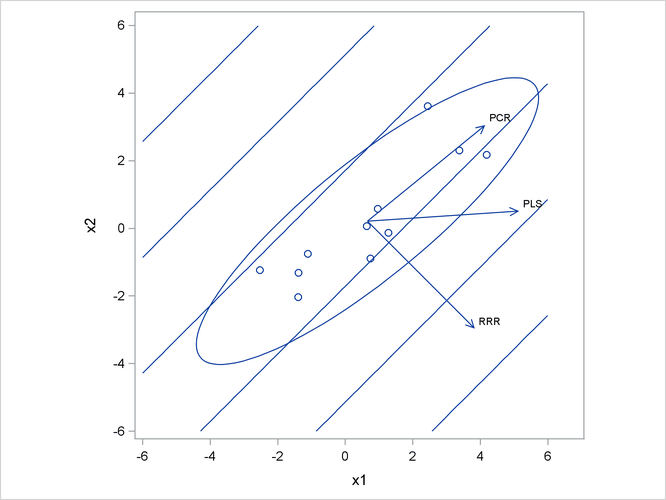
Figure 11.14 illustrates how partial least squares balances the goals of explaining response and predictor variation in this case.

Figure 11.14: Depiction of the First Factors for Three Different Regression Methods

The ellipse shows the general shape of the 11 observations in the predictor space, with the contours of increasing y overlaid. Also shown are the directions of the first factor for each of the three methods. Notice that although the predictors vary most in the x1 = x2 direction, the response changes most in the orthogonal x1 = –x2 direction. This explains why the first principal component accounts for little variation in the response and why the first reduced rank regression factor accounts for little variation in the predictors. The direction of the first partial least squares factor represents a compromise between the other two directions.