The HPLMIXED Procedure

Estimating Fixed and Random Effects in the Mixed Model

ML and REML methods provide estimates of $\bG $ and $\bR $, which are denoted $\widehat{\bG }$ and $\widehat{\bR }$, respectively. To obtain estimates of $\bbeta $ and predicted values of $\bgamma $, the standard method is to solve the mixed model equations (Henderson, 1984):

\[ \left[\begin{array}{lr} \bX ’\widehat{\bR }^{-1}\bX & \bX ’\widehat{\bR }^{-1}\bZ \\*\bZ ’\widehat{\bR }^{-1}\bX & \bZ ’\widehat{\bR }^{-1}\bZ + \widehat{\bG }^{-1} \end{array}\right] \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\bgamma } \end{array} \right] = \left[\begin{array}{r} \bX ’\widehat{\bR }^{-1}\mb{y} \\ \bZ ’\widehat{\bR }^{-1}\mb{y} \end{array} \right] \]

The solutions can also be written as

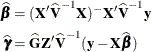
\begin{align*} \widehat{\bbeta } & = (\bX ’\widehat{\bV }^{-1}\bX )^{-} \bX ’\widehat{\bV }^{-1}\mb{y} \\ \widehat{\bgamma } & = \widehat{\bG }\bZ ’\widehat{\bV }^{-1} (\mb{y} - \bX \widehat{\bbeta }) \end{align*}

and have connections with empirical Bayes estimators (Laird and Ware, 1982; Carlin and Louis, 1996). Note that the $\bgamma $ are random variables and not parameters (unknown constants) in the model. Technically, determining values for $\bgamma $ from the data is thus a prediction task, whereas determining values for $\bbeta $ is an estimation task.

The mixed model equations are extended normal equations. The preceding expression assumes that $\widehat{\bG }$ is nonsingular. For the extreme case where the eigenvalues of $\widehat{\bG }$ are very large, $\widehat{\bG }^{-1}$ contributes very little to the equations and $\widehat{\bgamma }$ is close to what it would be if $\bgamma $ actually contained fixed-effects parameters. On the other hand, when the eigenvalues of $\widehat{\bG }$ are very small, $\widehat{\bG }^{-1}$ dominates the equations and $\widehat{\bgamma }$ is close to 0. For intermediate cases, $\widehat{\bG }^{-1}$ can be viewed as shrinking the fixed-effects estimates of $\bgamma $ toward 0 (Robinson, 1991).

If $\widehat{\bG }$ is singular, then the mixed model equations are modified (Henderson, 1984) as follows:

\[ \left[\begin{array}{lr} \bX ’\widehat{\bR } ^{-1}\bX & \bX ’\widehat{\bR } ^{-1} \bZ \widehat{\bG } \\ \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\bX & \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\bZ \widehat{\bG } + \bG \end{array}\right] \left[\begin{array}{c} \widehat{\bbeta } \\ \widehat{\btau } \end{array} \right] = \left[\begin{array}{r} \bX ’\widehat{\bR } ^{-1}\mb{y} \\ \widehat{\bG }’\bZ ’\widehat{\bR } ^{-1}\mb{y} \end{array} \right] \]

Denote the generalized inverses of the nonsingular $\widehat{\bG }$ and singular $\widehat{\bG }$ forms of the mixed model equations by $\bC $ and $\bM $, respectively. In the nonsingular case, the solution $\widehat{\bgamma }$ estimates the random effects directly. But in the singular case, the estimates of random effects are achieved through a back-transformation $\widehat{\bgamma } = \widehat{\bG }\widehat{\btau }$ where $\widehat{\btau }$ is the solution to the modified mixed model equations. Similarly, while in the nonsingular case $\bC $ itself is the estimated covariance matrix for $(\widehat{\bbeta },\widehat{\bgamma })$, in the singular case the covariance estimate for $(\widehat{\bbeta },\widehat{\bG }\widehat{\btau })$ is given by $\bP \bM \bP $ where

\[ \bP = \left[\begin{array}{cc} \bI & \\ & \widehat{\bG } \end{array}\right] \]

An example of when the singular form of the equations is necessary is when a variance component estimate falls on the boundary constraint of 0.