The HPFMM Procedure

The Form of the Finite Mixture Model

Suppose that you observe realizations of a random variable Y, the distribution of which depends on an unobservable random variable S that has a discrete distribution. S can occupy one of k states, the number of which might be unknown but is at least known to be finite. Since S is not observable, it is frequently referred to as a latent variable.

Let $\pi _ j$ denote the probability that S takes on state j. Conditional on $S=j$ , the distribution of the response Y is assumed to be $f_ j(y;\alpha _ j,\bbeta _ j|S=j)$ . In other words, each distinct state j of the random variable S leads to a particular distributional form $f_ j$ and set of parameters $\{ \alpha _ j,\bbeta _ j\}$ for Y.

Let $\{ \balpha , \bbeta \}$ denote the collection of $\alpha _ j$ and $\bbeta _ j$ parameters across all j = 1 to k. The marginal distribution of Y is obtained by summing the joint distribution of Y and S over the states in the support of S:

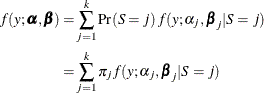
$\begin{align*} f(y;\balpha ,\bbeta ) =& \sum _{j=1}^ k \Pr (S=j)\, f(y;\alpha _ j,\bbeta _ j|S=j)\\ =& \sum _{j=1}^ k \pi _ j f(y;\alpha _ j,\bbeta _ j|S=j) \end{align*}$

This is a mixture of distributions, and the $\pi _ j$ are called the mixture (or prior) probabilities. Because the number of states k of the latent variable S is finite, the entire model is termed a finite mixture (of distributions) model.

The finite mixture model can be expressed in a more general form by representing $\balpha$ and $\bbeta$ in terms of regressor variables and parameters with optional additional scale parameters for $\bbeta$ . The section Notation for the Finite Mixture Model develops this in detail.