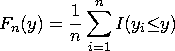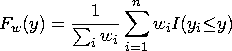Empirical CDF

Distribution Analyses

Empirical CDF

The empirical distribution function of a sample, F_n(y), is the proportion of observations less than or equal to y.

$F_{n}(y) = \frac{1}n \sum_{i=1}^n{I( y_{i} {\le} y)}$

where n is the number of observations, and $I(y_{i}\le y)$ is an indicator function with value 1 if $y_{i}\le y$ and with value 0 otherwise.

The Kolmogorov statistic D is a measure of the discrepancy between the empirical distribution and the hypothesized distribution.

$D = \rm{Max}_{y} {| F_{n}(y) - F(y)|}$

where F(y) is the hypothesized cumulative distribution function. The statistic is the maximum vertical distance between the two distribution functions. The Kolmogorov statistic can be used to construct a confidence band for the unknown distribution function, to test for a hypothesized completely known distribution, and to test for a specific family of distributions with unknown parameters.

If you select a Weight variable, the weighted empirical distribution function is the proportion of observation weights for observations less than or equal to y.

$F_{w}(y) = \frac{1}{\sum_{i}^{}{w_{i}}} \sum_{i=1}^n{w_{i} I( y_{i} {\le} y)}$

Top of Page