MRCHART Statement: SHEWHART Procedure

Creating Charts for Medians and Ranges from Raw Data

Note: See Median and Range Charts Examples in the SAS/QC Sample Library.

A consumer products company weighs detergent boxes (in pounds) to determine whether the fill process is in control. The following statements create a SAS data set named Detergent, which contains the weights for five boxes in each of 28 lots. A lot is considered a rational subgroup.

data Detergent;
   input Lot @;
   do i=1 to 5;
      input Weight @;
      output;
   end;
   drop i;
   datalines;
 1 17.39 26.93 19.34 22.56 24.49
 2 23.63 23.57 23.54 20.56 22.17
 3 24.35 24.58 23.79 26.20 21.55
 4 25.52 28.02 28.44 25.07 23.39
 5 23.25 21.76 29.80 23.09 23.70
 6 23.01 22.67 24.70 20.02 26.35
 7 23.86 24.19 24.61 26.05 24.18
 8 26.00 26.82 28.03 26.27 25.85
 9 21.58 22.31 25.03 20.86 26.94
10 22.64 21.05 22.66 29.26 25.02
11 26.38 27.50 23.91 26.80 22.53
12 23.01 23.71 25.26 20.21 22.38
13 23.15 23.53 22.98 21.62 26.99
14 26.83 23.14 24.73 24.57 28.09
15 26.15 26.13 20.57 25.86 24.70
16 25.81 23.22 23.99 23.91 27.57
17 25.53 22.87 25.22 24.30 20.29
18 24.88 24.15 25.29 29.02 24.46
19 22.32 25.96 29.54 25.92 23.44
20 25.63 26.83 20.95 24.80 27.25
21 21.68 21.11 26.07 25.17 27.63
22 26.72 27.05 24.90 30.08 25.22
23 31.58 22.41 23.67 23.47 24.90
24 28.06 23.44 24.92 24.64 27.42
25 21.10 22.34 24.96 26.50 24.51
26 23.80 24.03 24.75 24.82 27.21
27 25.10 26.09 27.21 24.28 22.45
28 25.53 22.79 26.26 25.85 25.64
;

A partial listing of Detergent is shown in Figure 18.43.

Figure 18.43: Partial Listing of the Data Set Detergent

The Data Set DETERGENT

Lot	Weight
1	17.39
1	26.93
1	19.34
1	22.56
1	24.49
2	23.63
2	23.57
2	23.54
2	20.56
2	22.17
3	24.35
3	24.58
3	23.79
3	26.20
3	21.55
4	25.52

The data set Detergent is said to be in "strung-out" form, because each observation contains the lot number and weight of a single box. The first five observations contain the weights for the first lot, the second five observations contain the weights for the second lot, and so on. Because the variable Lot classifies the observations into rational subgroups, it is referred to as the subgroup-variable. The variable Weight contains the weights and is referred to as the process variable (or process for short).

You can use median and range charts to determine whether the fill process is in control. The following statements create the charts shown in Figure 18.44:

ods graphics off;
title 'Median and Range Charts for Detergent Box Weight';
proc shewhart data=Detergent;
   mrchart Weight*Lot ;
run;

This example illustrates the basic form of the MRCHART statement. After the keyword MRCHART, you specify the process to analyze (in this case, Weight) followed by an asterisk and the subgroup-variable (Lot).

The input data set is specified with the DATA= option in the PROC SHEWHART statement.

Figure 18.44: Median and Range Charts (Traditional Graphics)

Each point on the median chart represents the median of the measurements for a particular lot. For instance, the weights for the first lot are 17.39, 19.34, 22.56, 24.49, and 26.93, and consequently, the median plotted for this lot is 22.56. Each point on the range chart represents the range of the measurements for a particular batch. For instance, the range plotted for the first lot is 26.93 – 17.39 = 9.54. Because all of the points lie within the control limits, you can conclude that the process is in statistical control.

By default, the control limits shown are 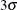$3\sigma$ limits estimated from the data; the formulas for the limits are given in Table 18.28. You can also read control limits from an input data set; see Reading Preestablished Control Limits.

For computational details, see Constructing Charts for Medians and Ranges. For more details on reading raw data, see DATA= Data Set.