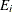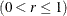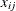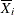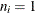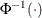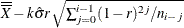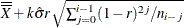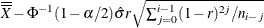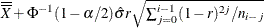EWMACHART Statement: MACONTROL Procedure
Constructing EWMA Charts
The following notation is used in this section:
|
|
Exponentially weighted moving average for the ith subgroup |
|
r |
EWMA weight parameter |
|
|
Process mean (expected value of the population of measurements) |
|
|
Process standard deviation (standard deviation of the population of measurements) |
|
|
jth measurement in ith subgroup, with j =1, 2, 3, …, |
|
|
Sample size of ith subgroup |
|
|
Mean of measurements in ith subgroup. If |
|
|
Weighted average of subgroup means |
|
|
Inverse standard normal function |
Plotted Points
Each point on the chart indicates the value of the exponentially weighted moving average (EWMA) for that subgroup. The EWMA
for the ith subgroup (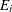 ) is defined recursively as
) is defined recursively as
![\[ E_{i}=r\overline{X}_{i}+(1-r)E_{i-1} \, , \; \; i>0 \]](images/qcug_macontrol0032.png)
where r is a weight parameter 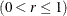 . Some authors (for example, Hunter 1986 and Crowder 1987a,b) use the symbol
. Some authors (for example, Hunter 1986 and Crowder 1987a,b) use the symbol 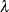 instead of r for the weight. You can specify the weight with the WEIGHT= option in the EWMACHART statement or with the variable _WEIGHT_
in a LIMITS= data set. If you specify a known value (
instead of r for the weight. You can specify the weight with the WEIGHT= option in the EWMACHART statement or with the variable _WEIGHT_
in a LIMITS= data set. If you specify a known value (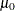 ) for
) for 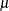 ,
, 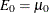 ; otherwise,
; otherwise, 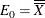 .
.
The preceding equation can be rewritten as
![\[ E_{i}=E_{i-1}+r(\overline{X}_{i}-E_{i-1}) \]](images/qcug_macontrol0036.png)
which expresses the current EWMA as the previous EWMA plus the weighted error in the prediction of the current mean based on the previous EWMA.
The EWMA for the ith subgroup can also be written as
![\[ E_{i}=r {\textstyle \sum _{j=0}^{i-1}}(1-r)^{j} \overline{X}_{i-j} +(1-r)^{i}E_{0} \]](images/qcug_macontrol0037.png)
which expresses the EWMA as a weighted average of past subgroup means, where the weights decline exponentially, and the heaviest weight is assigned to the most recent subgroup mean.
Central Line
By default, the central line on an EWMA chart indicates an estimate for 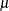 , which is computed as
, which is computed as
![\[ \hat{\mu }=\overline{\overline{X}} = \frac{n_{1}\bar{X_{1}} + \cdots + n_{N}\bar{X_{N}}}{n_{1} + \cdots + n_{N}} \]](images/qcug_macontrol0038.png)
If you specify a known value (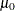 ) for
) for 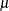 , the central line indicates the value of
, the central line indicates the value of 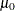 .
.
Control Limits
You can compute the limits in the following ways:
-
as a specified multiple (k) of the standard error of
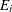 above and below the central line. The default limits are computed with k = 3 (these are referred to as
above and below the central line. The default limits are computed with k = 3 (these are referred to as 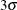 limits).
limits).
-
as probability limits defined in terms of
 , a specified probability that
, a specified probability that 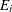 exceeds the limits
exceeds the limits
Table 9.4 presents the formulas for the limits.
Table 9.4: Limits for an EWMA Chart
|
Control Limits |
|---|
|
LCL = lower limit = |
|
UCL = upper limit = |
|
Probability Limits |
|
LCL = lower limit = |
|
UCL = upper limit = |
These formulas assume that the data are normally distributed. If standard values 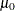 and
and 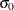 are available for
are available for 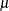 and
and  , respectively, replace
, respectively, replace 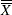 with
with 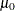 and
and 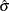 with
with 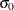 in Table 9.4. Note that the limits vary with both
in Table 9.4. Note that the limits vary with both 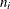 and i.
and i.
If the subgroup sample sizes are constant (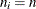 ), the formulas for the control limits simplify to
), the formulas for the control limits simplify to
![\[ \mr{LCL} = \overline{\overline{X}}-k\hat{\sigma }\sqrt {r(1-(1-r)^{2i})/n(2-r) } \]](images/qcug_macontrol0045.png)
![\[ \mr{UCL} = \overline{\overline{X}}+k\hat{\sigma }\sqrt {r(1-(1-r)^{2i})/n(2-r) } \]](images/qcug_macontrol0046.png)
Consequently, when the subgroup sample sizes are constant, the width of the control limits increases monotonically with i. For probability limits, replace k with 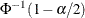 in the previous equations. Refer to Roberts (1959) and Montgomery (1996).
in the previous equations. Refer to Roberts (1959) and Montgomery (1996).
As i becomes large, the upper and lower control limits approach constant values:
![\[ \mr{LCL} = \overline{\overline{X}}-k\hat{\sigma }\sqrt {r/n(2-r) } \]](images/qcug_macontrol0015.png)
![\[ \mr{UCL} = \overline{\overline{X}}+k\hat{\sigma }\sqrt {r/n(2-r) } \]](images/qcug_macontrol0016.png)
Some authors base the control limits for EWMA charts on the asymptotic expressions in the two previous equations. For asymptotic
probability limits, replace k with 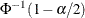 in these equations. You can display asymptotic limits by specifying the ASYMPTOTIC option.
in these equations. You can display asymptotic limits by specifying the ASYMPTOTIC option.
Uniformly weighted moving average charts and exponentially weighted moving average charts have similar properties, and their asymptotic control limits are identical provided that
![\[ r=2/(w+1) \]](images/qcug_macontrol0047.png)
where w is the weight factor for uniformly weighted moving average charts. Refer to Wadsworth, Stephens, and Godfrey (1986) and the American Society for Quality Control (1983).
You can specify parameters for the EWMA limits as follows:
-
Specify k with the SIGMAS= option or with the variable
_SIGMAS_in a LIMITS= data set. -
Specify
 with the ALPHA= option or with the variable
with the ALPHA= option or with the variable _ALPHA_in a LIMITS= data set. -
Specify a constant nominal sample size
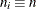 for the control limits with the LIMITN= option or with the variable
for the control limits with the LIMITN= option or with the variable _LIMITN_in a LIMITS= data set. -
Specify r with the WEIGHT= option or with the variable
_WEIGHT_in a LIMITS= data set. -
Specify
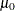 with the MU0= option or with the variable
with the MU0= option or with the variable _MEAN_in a LIMITS= data set. -
Specify
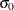 with the SIGMA0= option or with the variable
with the SIGMA0= option or with the variable _STDDEV_in a LIMITS= data set.
Choosing the Value of the Weight Parameter
Various approaches have been proposed for choosing the value of r.
-
Hunter (1986) states that the choice "can be left to the judgment of the quality control analyst" and points out that the smaller the value of r, "the greater the influence of the historical data."
-
Hunter (1986) also discusses a least squares procedure for estimating r from the data, assuming an exponentially weighted moving average model for the data. In this context, the fitted EWMA model provides a forecast of the process that is the basis for dynamic process control. You can use the ARIMA procedure in SAS/ETS® software to compute the least squares estimate of r. (Refer to SAS/ETS User's Guide for information about PROC ARIMA.) Also see Autocorrelation in Process Data.
-
A number of authors have studied the design of EWMA control schemes based on average run length (ARL) computations. The ARL is the expected number of points plotted before a shift is detected. Ideally, the ARL should be short when a shift occurs, and it should be long when there is no shift (the process is in control.) The effect of r on the ARL was described by Roberts (1959), who used simulation methods. The ARL function was approximated and tabulated by Robinson and Ho (1978), and a more general method for studying run-length distributions of EWMA charts was given by Crowder (1987a, 1987b). Unlike Hunter (1986), these authors assume the data are independent and identically distributed; typically the normal distribution is assumed for the data, although the methods extend to nonnormal distributions. A more detailed discussion of the ARL approach follows.
Average run lengths for two-sided EWMA charts are shown in Table 9.5, which is patterned after Table 1 of Crowder (1987a, 1987b). The ARLs were computed using the EWMAARL DATA step function (see EWMAARL Function for details on the EWMAARL function). Note that Crowder (1987a, 1987b). uses the notation L in place of k and the notation 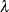 in place of r.
in place of r.
You can use Table 9.5 to find a combination of k and r that yields a desired ARL for an in-control process (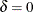 ) and for a specified shift of
) and for a specified shift of 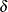 . Note that
. Note that 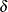 is assumed to be standardized; in other words, if a shift of
is assumed to be standardized; in other words, if a shift of 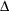 is to be detected in the process mean
is to be detected in the process mean 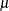 , and if
, and if  is the process standard deviation, you should select the table entry with
is the process standard deviation, you should select the table entry with
![\[ \delta =\Delta /(\sigma /\sqrt {n}) \]](images/qcug_macontrol0052.png)
where n is the subgroup sample size. Thus, 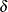 can be regarded as the shift in the sampling distribution of the subgroup mean.
can be regarded as the shift in the sampling distribution of the subgroup mean.
For example, suppose you want to construct an EWMA scheme with an in-control ARL of 90 and an ARL of 9 for detecting a shift
of 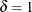 . Table 9.5 shows that the combination r = 0.5 and k = 2.5 yields an in-control ARL of 91.17 and an ARL of 8.27 for
. Table 9.5 shows that the combination r = 0.5 and k = 2.5 yields an in-control ARL of 91.17 and an ARL of 8.27 for 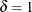 .
.
Crowder (1987a, 1987b) cautions that setting the in-control ARL at a desired level does not guarantee that the probability of an early false signal is acceptable. For further details concerning the distribution of the ARL, refer to Crowder (1987a, 1987b).
In addition to using Table 9.5 or the EWMAARL DATA step function to choose a EWMA scheme with desired average run length properties, you can use them to
evaluate an existing EWMA scheme. For example, the "Getting Started" section of this chapter contains EWMA schemes with r = 0.3 and k = 3. The following statements use the EWMAARL function to compute the in-control ARL and the ARLs for shifts of 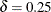 and
and 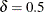 :
:
data arlewma; arlin = ewmaarl( 0,0.3,3.0); arl1 = ewmaarl(.25,0.3,3.0); arl2 = ewmaarl(.50,0.3,3.0); run;
The in-control ARL is 465.553, the ARL for 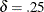 is 178.741, and the ARL for
is 178.741, and the ARL for 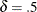 is 53.1603. See Example 9.5 for an illustration of how to use the EWMAARL function to compute average run lengths for various EWMA schemes and shifts.
is 53.1603. See Example 9.5 for an illustration of how to use the EWMAARL function to compute average run lengths for various EWMA schemes and shifts.
Table 9.5: Average Run Lengths for Two-Sided EWMA Charts
|
r (weight parameter) |
|||||||
|---|---|---|---|---|---|---|---|
|
k |
|
0.05 |
0.10 |
0.25 |
0.50 |
0.75 |
1.00 |
|
2.0 |
0.00 |
127.53 |
73.28 |
38.56 |
26.45 |
22.88 |
21.98 |
|
2.0 |
0.25 |
43.94 |
34.49 |
24.83 |
20.12 |
18.86 |
19.13 |
|
2.0 |
0.50 |
18.97 |
15.53 |
12.74 |
11.89 |
12.34 |
13.70 |
|
2.0 |
0.75 |
11.64 |
9.36 |
7.62 |
7.29 |
7.86 |
9.21 |
|
2.0 |
1.00 |
8.38 |
6.62 |
5.24 |
4.91 |
5.26 |
6.25 |
|
2.0 |
1.25 |
6.56 |
5.13 |
3.96 |
3.59 |
3.76 |
4.40 |
|
2.0 |
1.50 |
5.41 |
4.20 |
3.19 |
2.80 |
2.84 |
3.24 |
|
2.0 |
1.75 |
4.62 |
3.57 |
2.68 |
2.29 |
2.26 |
2.49 |
|
2.0 |
2.00 |
4.04 |
3.12 |
2.32 |
1.95 |
1.88 |
2.00 |
|
2.0 |
2.25 |
3.61 |
2.78 |
2.06 |
1.70 |
1.61 |
1.67 |
|
2.0 |
2.50 |
3.26 |
2.52 |
1.85 |
1.51 |
1.42 |
1.45 |
|
2.0 |
2.75 |
2.99 |
2.32 |
1.69 |
1.37 |
1.29 |
1.29 |
|
2.0 |
3.00 |
2.76 |
2.16 |
1.55 |
1.26 |
1.19 |
1.19 |
|
2.0 |
3.25 |
2.56 |
2.03 |
1.43 |
1.18 |
1.13 |
1.12 |
|
2.0 |
3.50 |
2.39 |
1.93 |
1.32 |
1.12 |
1.08 |
1.07 |
|
2.0 |
3.75 |
2.26 |
1.83 |
1.24 |
1.08 |
1.05 |
1.04 |
|
2.0 |
4.00 |
2.15 |
1.73 |
1.17 |
1.05 |
1.03 |
1.02 |
|
2.5 |
0.00 |
379.09 |
223.35 |
124.18 |
91.17 |
82.49 |
80.52 |
|
2.5 |
0.25 |
73.98 |
66.59 |
59.66 |
58.33 |
61.07 |
65.77 |
|
2.5 |
0.50 |
26.63 |
23.63 |
23.28 |
27.16 |
33.26 |
41.49 |
|
2.5 |
0.75 |
15.41 |
12.95 |
11.96 |
13.96 |
18.05 |
24.61 |
|
2.5 |
1.00 |
10.79 |
8.75 |
7.52 |
8.27 |
10.57 |
14.92 |
|
2.5 |
1.25 |
8.31 |
6.60 |
5.39 |
5.52 |
6.75 |
9.46 |
|
2.5 |
1.50 |
6.78 |
5.31 |
4.18 |
4.03 |
4.65 |
6.30 |
|
2.5 |
1.75 |
5.75 |
4.46 |
3.43 |
3.14 |
3.43 |
4.41 |
|
2.5 |
2.00 |
5.00 |
3.86 |
2.92 |
2.57 |
2.67 |
3.24 |
|
2.5 |
2.25 |
4.43 |
3.42 |
2.56 |
2.18 |
2.17 |
2.49 |
|
2.5 |
2.50 |
4.00 |
3.07 |
2.29 |
1.90 |
1.83 |
2.00 |
|
2.5 |
2.75 |
3.64 |
2.80 |
2.08 |
1.69 |
1.59 |
1.67 |
|
2.5 |
3.00 |
3.36 |
2.57 |
1.91 |
1.52 |
1.41 |
1.45 |
|
2.5 |
3.25 |
3.12 |
2.39 |
1.77 |
1.39 |
1.29 |
1.29 |
|
2.5 |
3.50 |
2.92 |
2.24 |
1.64 |
1.28 |
1.19 |
1.19 |
|
2.5 |
3.75 |
2.74 |
2.13 |
1.52 |
1.20 |
1.13 |
1.12 |
|
2.5 |
4.00 |
2.58 |
2.04 |
1.42 |
1.13 |
1.08 |
1.07 |
|
3.0 |
0.00 |
1383.62 |
842.15 |
502.90 |
397.46 |
374.50 |
370.40 |
|
3.0 |
0.25 |
133.61 |
144.74 |
171.09 |
208.54 |
245.76 |
281.15 |
|
3.0 |
0.50 |
37.33 |
37.41 |
48.45 |
75.35 |
110.95 |
155.22 |
|
3.0 |
0.75 |
19.95 |
17.90 |
20.16 |
31.46 |
50.92 |
81.22 |
|
3.0 |
1.00 |
13.52 |
11.38 |
11.15 |
15.74 |
25.64 |
43.89 |
|
3.0 |
1.25 |
10.24 |
8.32 |
7.39 |
9.21 |
14.26 |
24.96 |
|
3.0 |
1.50 |
8.26 |
6.57 |
5.47 |
6.11 |
8.72 |
14.97 |
|
3.0 |
1.75 |
6.94 |
5.45 |
4.34 |
4.45 |
5.80 |
9.47 |
|
3.0 |
2.00 |
6.00 |
4.67 |
3.62 |
3.47 |
4.15 |
6.30 |
|
3.0 |
2.25 |
5.30 |
4.10 |
3.11 |
2.84 |
3.16 |
4.41 |
|
3.0 |
2.50 |
4.76 |
3.67 |
2.75 |
2.41 |
2.52 |
3.24 |
|
3.0 |
2.75 |
4.32 |
3.32 |
2.47 |
2.10 |
2.09 |
2.49 |
|
3.0 |
3.00 |
3.97 |
3.05 |
2.26 |
1.87 |
1.79 |
2.00 |
|
3.0 |
3.25 |
3.67 |
2.82 |
2.09 |
1.69 |
1.57 |
1.67 |
|
3.0 |
3.50 |
3.42 |
2.62 |
1.95 |
1.53 |
1.41 |
1.45 |
|
3.0 |
3.75 |
3.22 |
2.45 |
1.84 |
1.41 |
1.29 |
1.29 |
|
3.0 |
4.00 |
3.04 |
2.30 |
1.73 |
1.31 |
1.20 |
1.19 |
|
3.5 |
0.00 |
12851.0 |
4106.4 |
2640.16 |
2227.34 |
2157.99 |
2149.34 |
|
3.5 |
0.25 |
281.09 |
381.29 |
625.78 |
951.18 |
1245.90 |
1502.76 |
|
3.5 |
0.50 |
53.58 |
64.72 |
123.43 |
267.36 |
468.68 |
723.81 |
|
3.5 |
0.75 |
25.62 |
25.33 |
38.68 |
88.70 |
182.12 |
334.40 |
|
3.5 |
1.00 |
16.65 |
14.79 |
17.71 |
35.97 |
78.05 |
160.95 |
|
3.5 |
1.25 |
12.36 |
10.37 |
10.48 |
17.64 |
37.15 |
81.80 |
|
3.5 |
1.50 |
9.86 |
8.00 |
7.25 |
10.19 |
19.63 |
43.96 |
|
3.5 |
1.75 |
8.22 |
6.54 |
5.52 |
6.70 |
11.46 |
24.96 |
|
3.5 |
2.00 |
7.07 |
5.55 |
4.47 |
4.86 |
7.33 |
14.97 |
|
3.5 |
2.25 |
6.21 |
4.83 |
3.77 |
3.78 |
5.08 |
9.47 |
|
3.5 |
2.50 |
5.55 |
4.29 |
3.28 |
3.10 |
3.76 |
6.30 |
|
3.5 |
2.75 |
5.03 |
3.87 |
2.91 |
2.63 |
2.94 |
4.41 |
|
3.5 |
3.00 |
4.60 |
3.54 |
2.63 |
2.30 |
2.40 |
3.24 |
|
3.5 |
3.25 |
4.25 |
3.26 |
2.41 |
2.05 |
2.03 |
2.49 |
|
3.5 |
3.50 |
3.95 |
3.03 |
2.23 |
1.85 |
1.76 |
2.00 |
|
3.5 |
3.75 |
3.70 |
2.84 |
2.10 |
1.69 |
1.56 |
1.67 |
|
3.5 |
4.00 |
3.47 |
2.66 |
1.99 |
1.55 |
1.40 |
1.45 |