Functions
C4 Function
computes the expected value of the standard deviation of n independent normal random variables.
Syntax
C4(n)
where n is the sample size, with 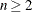 .
.
Description
The C4 function returns the expected value of the standard deviation of n independent, normally distributed random variables with the same mean and with standard deviation of 1. This expected value
is referred to as the control chart constant 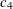 .
.
The value 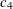 is calculated as
is calculated as
![\[ c_4 = \frac{\Gamma (\frac{n}{2}) \sqrt {2/(n-1) } }{\Gamma (\frac{n-1}{2}) } \]](images/qcug_functions0050.png)
where 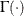 is the gamma function. As n grows,
is the gamma function. As n grows, 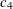 is asymptotically equal to
is asymptotically equal to 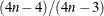 .
.
For more information, refer to the American Society for Quality Control (1983), the American Society for Testing and Materials (1976), Montgomery (1996), and Wadsworth, Stephens, and Godfrey (1986).
In other chapters, 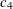 is written as
is written as 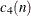 to emphasize the dependence on n.
to emphasize the dependence on n.
You can use the constant 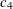 to calculate an unbiased estimate
to calculate an unbiased estimate 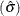 of the standard deviation
of the standard deviation  of a normal distribution from the sample standard deviation of n observations:
of a normal distribution from the sample standard deviation of n observations:
![\[ \hat{\sigma } = (\mbox{sample standard deviation})/c_4 \]](images/qcug_functions0055.png)
where the sample standard deviation is calculated using n – 1 in the denominator. In the SHEWHART procedure, 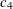 is used to calculate control limits for s charts, and it is used in the estimation of the process standard deviation based on subgroup standard deviations.
is used to calculate control limits for s charts, and it is used in the estimation of the process standard deviation based on subgroup standard deviations.