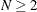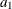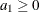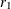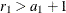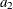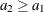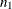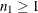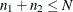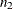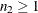Functions
ATI2 Function
computes the average total inspection for a double-sampling plan.
Syntax
ATI2(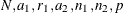 )
)
where
|
N |
is the lot size, where |
|
|
is the acceptance number for the first sample, where |
|
|
is the rejection number for the first sample, where |
|
|
is the acceptance number for the second sample, where |
|
|
is the size of the first sample, where |
|
|
is the size of the second sample, where |
|
p |
is the proportion of nonconforming items produced by the process, where 0 < p < 1. |
Description
The ATI2 function returns the average total inspection for a Type B double-sampling plan. For details on Type B double-sampling plans, see Types of Sampling Plans.
The average total inspection is
![\[ \mbox{ATI}=n_1P_{a_1}+(n_1+n_2)P_{a_2}+N(1-P_{a_1}-P_{a_2}) \]](images/qcug_functions0025.png)
where
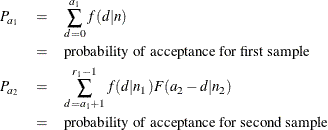
and