The MVPMONITOR Procedure
This example is a continuation of the example in Getting Started: MVPMONITOR Procedure. The following statements create a data set named flightDelays2, which provides flight delays for the date range February 17–28, 2007, for the northeastern United States:
data flightDelays2; label flightDate='Date'; format flightDate MMDDYY8.; input flightDate :MMDDYY8. AA CO DL F9 FL NW UA US WN; datalines; 02/17/07 25.6 7.8 15.5 13.4 16.1 16.2 23.0 24.2 8.2 02/18/07 5.4 16.0 9.9 1.1 11.5 17.0 15.6 15.5 5.1 02/19/07 13.2 16.3 10.0 10.6 5.4 10.3 9.5 16.8 9.3 02/20/07 4.2 6.9 1.4 0.1 7.2 6.6 7.4 10.4 2.9 02/21/07 5.4 -0.1 7.4 8.7 16.3 24.3 9.4 6.0 10.2 02/22/07 19.6 30.2 6.8 2.7 8.9 16.4 14.3 12.6 8.2 02/23/07 14.9 18.9 9.9 9.1 12.0 16.5 17.4 12.8 6.0 02/24/07 21.4 5.5 11.1 46.1 10.6 55.3 22.9 8.8 3.4 02/25/07 42.6 7.7 14.6 14.4 32.0 50.7 46.1 49.4 39.1 02/26/07 43.2 25.1 18.1 18.2 28.8 31.1 38.6 29.6 18.6 02/27/07 11.3 17.1 5.3 4.1 4.8 13.9 9.8 9.7 7.1 02/28/07 8.1 3.7 2.7 17.1 -0.8 5.5 11.0 14.3 3.1 ;
To use PROC MVPMONITOR in a Phase II analysis, you need a principal component model based on a process data from a stable
process. The model that is produced by the MVPMODEL procedure in Combining Data from Peer Processes is used here. The model was generated from data for the continental United States during February 1–16, 2007. The model information
is contained in the principal component loadings, which come from the mvpairloadings data set. The following statements apply the model to the new data in flightDelays2:
proc mvpmonitor data=flightDelays2 loadings=mvpairloadings; time flightDate; id flightDate; tsquarechart; spechart; run;
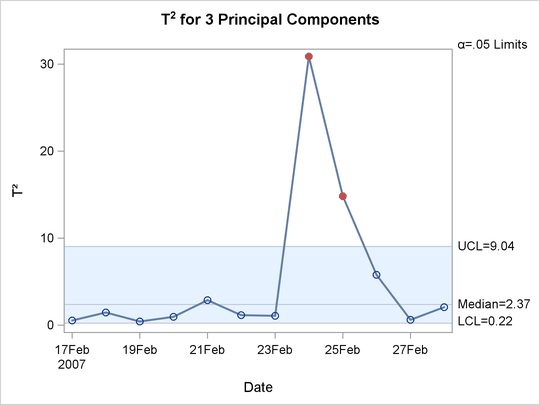
The ![]() chart is shown in Output 13.2.1.
chart is shown in Output 13.2.1.
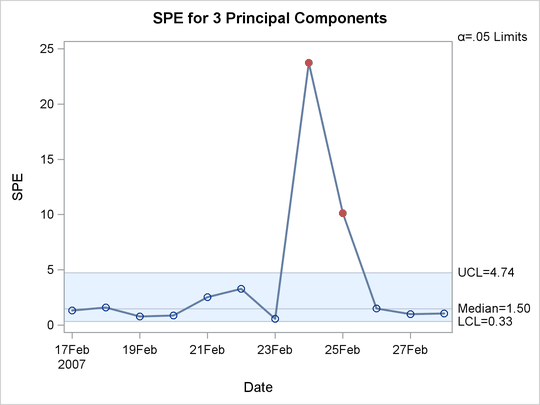
The SPE chart is shown in Output 13.2.2.
The SPE chart has out-of-control points on February 22, 24, and 25. This indicates that the variation is not along the model hyperplane, which suggests that the model is not appropriate for these new data.
Both the SPE chart and the ![]() chart have an out-of-control point on February 25. This point has very unusual variation. On that date, a major winter storm
with high winds and blizzard conditions battered the Midwest while snow, sleet, and freezing rain hit the Northeast. These
conditions contributed to delays that are not seen in the data set that the model was built with.
chart have an out-of-control point on February 25. This point has very unusual variation. On that date, a major winter storm
with high winds and blizzard conditions battered the Midwest while snow, sleet, and freezing rain hit the Northeast. These
conditions contributed to delays that are not seen in the data set that the model was built with.