Dictionary of Special Options :: SAS/QC(R) 13.1 User's Guide

Dictionary of Special Options

ALPHA=value

requests probability limits. If you specify ALPHA= $\alpha$ , the control limits are computed so that the probability is $\alpha$ that a single moving average exceeds its control limits. The value of $\alpha$ can range between 0 and 1. This assumes that the process is in statistical control and that the data follow a normal distribution. For the equations used to compute probability limits, see Control Limits.

Note the following:

As an alternative to specifying ALPHA= $\alpha$ , you can read $\alpha$ from the variable _ALPHA_ in a LIMITS= data set by specifying the READALPHA option.
As an alternative to specifying ALPHA= $\alpha$ (or reading _ALPHA_ from a LIMITS= data set), you can request “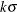 $k\sigma$ control limits” by specifying SIGMAS=k (or reading _SIGMAS_ from a LIMITS= data set).

If you specify neither the ALPHA= option nor the SIGMAS= option, the procedure computes 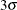$3\sigma$ control limits by default.

ASYMPTOTIC

requests constant upper and lower control limits for all subgroups having the following values:

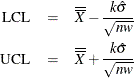
$\begin{eqnarray*} \textrm{LCL}& =& \overline{\overline{X}}-\frac{k\hat{\sigma }}{\sqrt {nw} } \\ \textrm{UCL}& =& \overline{\overline{X}}+\frac{k\hat{\sigma }}{\sqrt {nw} } \end{eqnarray*}$

Here w is the span of the moving average, and n is the nominal sample size associated with the control limits. Substitute 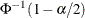$\Phi ^{-1}(1-\alpha /2)$ for k if you specify probability limits with the ALPHA= option. When you do not specify the ASYMPTOTIC option, the control limits are computed using the exact formulas in Table 9.9. Use the ASYMPTOTIC option only if all the subgroup sample sizes are the same or if you specify LIMITN=n.

CMEANSYMBOL=color

specifies the color used for the symbol requested with the MEANSYMBOL= option in traditional graphics. This option is ignored unless you are producing traditional graphics.

LIMITN=n LIMITN=VARYING

specifies either a fixed or varying nominal sample size for the control limits.

If you specify LIMITN=n, moving averages are calculated and displayed only for those subgroups with a sample size equal to n, unless you also specify the ALLN option, which causes all the moving averages to be calculated and displayed. By default (or if you specify LIMITN=VARYING), moving averages are calculated and displayed for all subgroups, regardless of sample size.

MEANCHAR='character'

specifies a character used in legacy line printer charts to plot the subgroup mean for each subgroup. By default, subgroup means are not plotted. This option is ignored unless you specify the LINEPRINTER option in the PROC MACONTROL statement.

MEANSYMBOL=keyword

specifies a symbol used to plot the subgroup mean for each subgroup in traditional graphics. By default, subgroup means are not plotted. This option is ignored unless you are producing traditional graphics.

MU0=value

specifies a known (standard) value 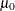$\mu _0$ for the process mean 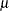$\mu$ . By default, 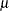$\mu$ is estimated from the data.

Note: As an alternative to specifying MU0= 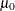$\mu _0$ , you can read a predetermined value for 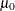$\mu _0$ from the variable _MEAN_ in a LIMITS= data set.

See Example 9.6.

NOREADLIMITS

specifies that control limit parameters for each process listed in the MACHART statement are not to be read from the LIMITS= data set specified in the PROC MACONTROL statement.

The following example illustrates the NOREADLIMITS option:

proc macontrol data=Pistons limits=Diamlim;
   machart Diameter*Hour;
   machart Diameter*Hour / noreadlimits span=3;
run;

The first MACHART statement reads the control limits from the first observation in the data set Diamlim for which the variable _VAR_ is equal to 'Diameter' and the variable _SUBGRP_ is equal to 'Hour'. The second MACHART statement computes estimates of the process mean and standard deviation for the control limits from the measurements in the data set Pistons. Note that the second MACHART statement is equivalent to the following statements, which would be more commonly used:

proc macontrol data=Pistons;
   machart Diameter*Hour / span=3;
run;

For more information about reading control limit parameters from a LIMITS= data set, see the READLIMITS option later in this list.

READALPHA

specifies that the variable _ALPHA_, rather than the variable _SIGMAS_, is to be read from a LIMITS= data set when both variables are available in the data set. Thus the limits displayed are probability limits. If you do not specify the READALPHA option, then _SIGMAS_ is read by default.

READINDEX=’value’

reads control limit parameters from a LIMITS= data set (specified in the PROC MACONTROL statement) for each process listed in the MACHART statement. The control limit parameters for a particular process are read from the first observation in the LIMITS= data set for which

the value of _VAR_ matches process
the value of _SUBGRP_ matches the subgroup-variable
the value of _INDEX_ matches value

The value can be up to 48 characters and must be enclosed in quotes.

READLIMITS

specifies that control limit parameters are to be read from a LIMITS= data set specified in the PROC MACONTROL statement. The parameters for a particular process are read from the first observation in the LIMITS= data set for which

the value of _VAR_ matches process
the value of _SUBGRP_ matches the subgroup variable

Note: In SAS 6.10 and later releases, the READLIMITS option is not necessary.

SIGMA0=value

specifies a known (standard) value 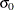$\sigma _0$ for the process standard deviation $\sigma$ . The value must be positive. By default, the MACONTROL procedure estimates $\sigma$ from the data using the formulas given in Methods for Estimating the Standard Deviation.

Note: As an alternative to specifying SIGMA0= 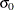$\sigma _0$ , you can read a predetermined value for 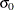$\sigma _0$ from the variable _STDDEV_ in a LIMITS= data set.

SIGMAS=value

specifies the width of the control limits in terms of the multiple k of the standard error of the plotted moving averages on the chart. The value of k must be positive. By default, k = 3 and the control limits are 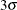$3\sigma$ limits.

SPAN=value

specifies the number of terms used to calculate the moving average (value is an integer greater than 1). The SPAN= option is required unless you read control limit parameters from a LIMITS= data set or a TABLE= data set. See Plotted Points and Choosing the Span of the Moving Average for details.

MACHART Statement: MACONTROL Procedure

Dictionary of Special Options