EWMACHART Statement: MACONTROL Procedure

Example 9.1 Specifying Standard Values for the Process Mean and Process Standard Deviation

Note: See Specifying Standard Values for EWMA Chart in the SAS/QC Sample Library.

By default, the EWMACHART statement estimates the process mean ( $\mu$ ) and standard deviation ( $\sigma$ ) from the data. This is illustrated in the “Getting Started” section of this chapter. However, there are applications in which standard values ( $\mu _0$ and $\sigma _0$ ) are available based, for instance, on previous experience or extensive sampling. You can specify these values with the MU0= and SIGMA0= options.

For example, suppose it is known that the metal clip manufacturing process (introduced in Creating EWMA Charts from Raw Data) has a mean of 15 and standard deviation of 0.2. The following statements specify these standard values:

ods graphics off;
title 'Specifying Standard Process Mean and Standard Deviation';
symbol v=dot h=0.8;
proc macontrol data=Clips1;
   ewmachart Gap*Day /
       mu0     = 15
       sigma0  = 0.2
       weight  = 0.3
       xsymbol = mu0;
run;

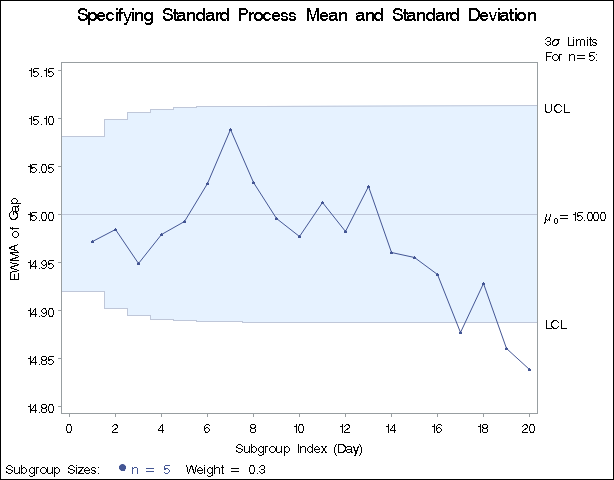
The XSYMBOL= option specifies the label for the central line. The resulting chart is shown in Output 9.1.1.

Output 9.1.1: Specifying Standard Values with MU0= and SIGMA0=

The central line and control limits are determined using $\mu _0$ and $\sigma _0$ (see the equations in Table 9.3). Output 9.1.1 indicates that the process is out-of-control, since the moving averages for Day=17, Day=19, and Day=20 lie below the lower control limit.

You can also specify $\mu _0$ and $\sigma _0$ with the variables _MEAN_ and _STDDEV_ in a LIMITS= data set, as illustrated by the following statements:

data Cliplim;
   length _var_ _subgrp_ _type_ $8;
   _var_    = 'Gap';
   _subgrp_ = 'Day';
   _type_   = 'STANDARD';
   _limitn_ = 5;
   _mean_   = 15;
   _stddev_ = 0.2;
   _weight_ = 0.3;

proc macontrol data=Clips1 limits=Cliplim;
   ewmachart Gap*Day / xsymbol=mu0;
run;

The variable _WEIGHT_ is required, and its value provides the weight parameter used to compute the EWMAs. The variables _VAR_ and _SUBGRP_ are also required, and their values must match the process and subgroup-variable, respectively, specified in the EWMACHART statement. The bookkeeping variable _TYPE_ is not required, but it is recommended to indicate that the variables _MEAN_ and _STDDEV_ provide standard values rather than estimated values.

The resulting chart (not shown here) is identical to the one shown in Output 9.1.1.