QQPLOT Statement: CAPABILITY Procedure
This example, which is a continuation of Example 5.21, demonstrates techniques for estimating the shape parameter, location and scale parameters, and theoretical percentiles for a lognormal distribution.
Note: See Creating Lognormal Q-Q Plots in the SAS/QC Sample Library.
The three-parameter lognormal distribution depends on a threshold parameter ![]() , a scale parameter
, a scale parameter ![]() , and a shape parameter
, and a shape parameter ![]() . You can estimate
. You can estimate ![]() from a series of lognormal Q-Q plots with different values of
from a series of lognormal Q-Q plots with different values of ![]() . The estimate is the value of
. The estimate is the value of ![]() that linearizes the point pattern. You can then estimate the threshold and scale parameters from the intercept and slope
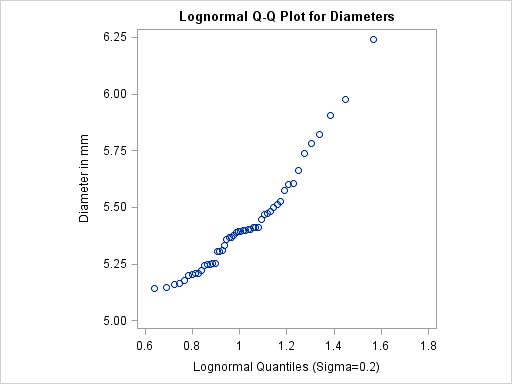
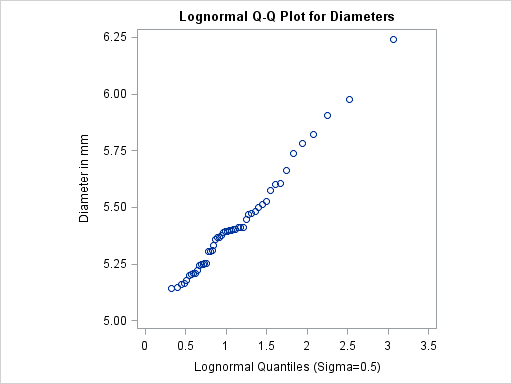
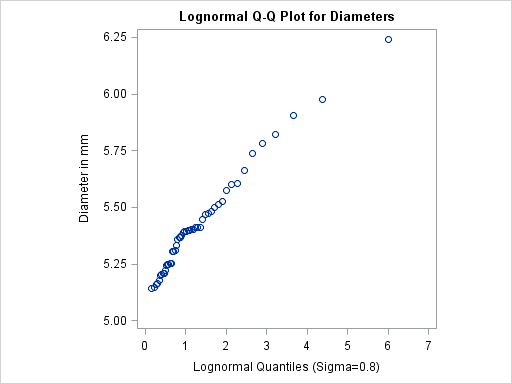
of the point pattern. The following statements create the series of plots in Output 5.22.1 through Output 5.22.3 for
that linearizes the point pattern. You can then estimate the threshold and scale parameters from the intercept and slope
of the point pattern. The following statements create the series of plots in Output 5.22.1 through Output 5.22.3 for ![]() values of 0.2, 0.5, and 0.8:
values of 0.2, 0.5, and 0.8:
title 'Lognormal Q-Q Plot for Diameters';
proc capability data=Measures noprint;
qqplot Diameter / lognormal(sigma=0.2 0.5 0.8)
square
odstitle=title;
run;
Note: You must specify a value for the shape parameter ![]() for a lognormal Q-Q plot with the SIGMA= option or its alias, the SHAPE= option.
for a lognormal Q-Q plot with the SIGMA= option or its alias, the SHAPE= option.
The plot in Output 5.22.2 displays the most linear point pattern, indicating that the lognormal distribution with ![]() provides a reasonable fit for the data distribution.
provides a reasonable fit for the data distribution.
Data with this particular lognormal distribution have the density function
![]()
The points in the plot fall on or near the line with intercept ![]() and slope
and slope ![]() . Based on Output 5.22.2,
. Based on Output 5.22.2, ![]() and
and ![]() , giving
, giving ![]() .
.
Note: See Creating Lognormal Q-Q Plots in the SAS/QC Sample Library.
You can use a Q-Q plot to estimate percentiles such as the 95th percentile of the lognormal distribution.[13]
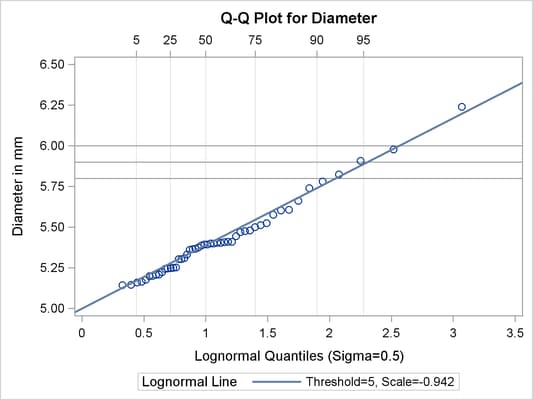
The point pattern in Output 5.22.2 has a slope of approximately 0.39 and an intercept of 5. The following statements reproduce this plot, adding a lognormal reference line with this slope and intercept.
title 'Lognormal Q-Q Plot for Diameters';
proc capability data=Measures noprint;
qqplot Diameter / lognormal(sigma=0.5 theta=5 slope=0.39)
pctlaxis(grid)
vref = 5.8 5.9 6.0;
run;
The ODS GRAPHICS ON statement specified before the PROC CAPABILITY statement enables ODS Graphics, so the Q-Q plot is created using ODS Graphics instead of traditional graphics. The result is shown in Output 5.22.4.
The PCTLAXIS option labels the major percentiles, and the GRID option draws percentile axis reference lines. The 95th percentile is 5.9, because the intersection of the distribution reference line and the 95th reference line occurs at this value on the vertical axis.
Alternatively, you can compute this percentile from the estimated lognormal parameters. The ![]() th percentile of the lognormal distribution is
th percentile of the lognormal distribution is
where ![]() is the inverse cumulative standard normal distribution. Consequently,
is the inverse cumulative standard normal distribution. Consequently,
Note: See Creating Lognormal Q-Q Plots in the SAS/QC Sample Library.
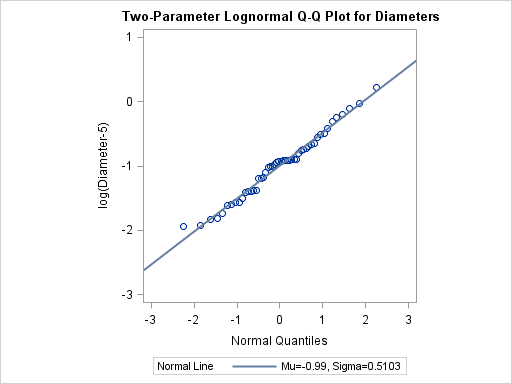
If a known threshold parameter is available, you can construct a two-parameter lognormal Q-Q plot by subtracting the threshold
from the data and requesting a normal Q-Q plot. The following statements create this plot for Diameter, assuming a known threshold of five:
data Measures; set Measures; Logdiam=log(Diameter-5); label Logdiam='log(Diameter-5)'; run;
title 'Two-Parameter Lognormal Q-Q Plot for Diameters';
proc capability data=Measures noprint;
qqplot Logdiam / normal(mu=est sigma=est)
square
odstitle=title;
run;
Because the point pattern in Output 5.22.5 is linear, you can estimate the lognormal parameters ![]() and
and ![]() as the normal plot estimates of
as the normal plot estimates of ![]() and
and ![]() , which are –0.99 and 0.51. These values correspond to the previous estimates of –0.92 for
, which are –0.99 and 0.51. These values correspond to the previous estimates of –0.92 for ![]() and 0.5 for
and 0.5 for ![]() .
.