UCHART Statement: SHEWHART Procedure
Constructing Charts for Nonconformities per Unit (u Charts)
The following notation is used in this section:
|
u |
expected number of nonconformities per unit produced by process |
|
|
|
number of nonconformities per unit in the ith subgroup. In general, |
|
|
|
total number of nonconformities in the ith subgroup |
|
|
|
number of inspection units in the ith subgroup |
|
|
|
average number of nonconformities per unit taken across subgroups. The quantity
|
|
|
N |
number of subgroups |
|
|
|
has a central |
Plotted Points
Each point on a u chart indicates the number of nonconformities per unit (![]() ) in a subgroup. For example, Figure 17.94 displays three sections of pipeline that are inspected for defective welds (indicated by an X). Each section represents a subgroup composed of a number of inspection units, which are 1000-foot-long sections. The number of units in the ith subgroup is denoted by
) in a subgroup. For example, Figure 17.94 displays three sections of pipeline that are inspected for defective welds (indicated by an X). Each section represents a subgroup composed of a number of inspection units, which are 1000-foot-long sections. The number of units in the ith subgroup is denoted by ![]() , which is the subgroup sample size.
, which is the subgroup sample size.
Figure 17.94: Terminology for c Charts and u Charts
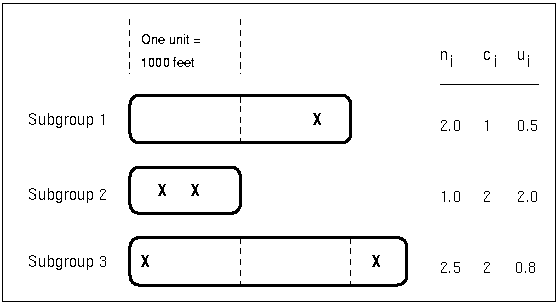
The number of nonconformities in the ith subgroup is denoted by ![]() . The number of nonconformities per unit in the ith subgroup is denoted by
. The number of nonconformities per unit in the ith subgroup is denoted by ![]() . In Figure 17.94, the number of defective welds per unit in the third subgroup is
. In Figure 17.94, the number of defective welds per unit in the third subgroup is ![]() .
.
A u chart plots the quantity ![]() for the ith subgroup. A c chart plots the quantity
for the ith subgroup. A c chart plots the quantity ![]() for the ith subgroup (see CCHART Statement: SHEWHART Procedure). An advantage of a u chart is that the value of the central line at the ith subgroup does not depend on
for the ith subgroup (see CCHART Statement: SHEWHART Procedure). An advantage of a u chart is that the value of the central line at the ith subgroup does not depend on ![]() . This is not the case for a c chart, and consequently, a u chart is often preferred when the number of units
. This is not the case for a c chart, and consequently, a u chart is often preferred when the number of units ![]() is not constant across subgroups.
is not constant across subgroups.
Central Line
On a u chart, the central line indicates an estimate of u, which is computed as ![]() by default. If you specify a known value (
by default. If you specify a known value (![]() ) for u, the central line indicates the value of
) for u, the central line indicates the value of ![]() .
.
Control Limits
You can compute the limits in the following ways:
-
as a specified multiple (k) of the standard error of
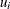 above and below the central line. The default limits are computed with k = 3 (these are referred to as
above and below the central line. The default limits are computed with k = 3 (these are referred to as 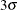 limits).
limits).
-
as probability limits defined in terms of
 , a specified probability that
, a specified probability that 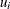 exceeds the limits
exceeds the limits
The lower and upper control limits, LCLU and UCLU, respectively, are given by
|
|
|
|
|
|
|
|
The limits vary with ![]() .
.
The upper probability limit UCLU for ![]() can be determined using the fact that
can be determined using the fact that
![\[ \begin{array}{ll} P\{ u_{i} > \mbox{UCLU}\} & = 1 - P\{ u_{i} \leq \mbox{UCLU} \} \\ & = 1 - P\{ c_{i} \leq n_{i}\mbox{UCLU} \} \\ & = 1 - P\{ \chi ^{2}_{2(n_{i}(\! {\mbox{\scriptsize UCLU}}+1))} \geq 2n_{i}\bar{u}\} \end{array} \]](images/qcug_shewhart0272.png) |
The limit UCLU is then calculated by setting
|
|
and solving for UCLU.
Likewise, the lower probability limit LCLC for ![]() can be determined using the fact that
can be determined using the fact that
|
|
The limit LCLC is then calculated by setting
|
|
and solving for LCLC. For more information, refer to Johnson, Kotz, and Kemp (1992). This assumes that the process is in statistical control and that ![]() has a Poisson distribution. Note that the probability limits vary with
has a Poisson distribution. Note that the probability limits vary with ![]() and are asymmetric around the central line. If a standard value
and are asymmetric around the central line. If a standard value ![]() is available for u, replace
is available for u, replace ![]() with
with ![]() in the formulas for the control limits.
in the formulas for the control limits.
You can specify parameters for the limits as follows:
-
Specify k with the SIGMAS= option or with the variable
_SIGMAS_in a LIMITS= data set. -
Specify
 with the ALPHA= option or with the variable
with the ALPHA= option or with the variable _ALPHA_in a LIMITS= data set. -
Specify a constant nominal sample size
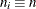 for the control limits with the LIMITN= option or with the variable
for the control limits with the LIMITN= option or with the variable _LIMITN_in a LIMITS= data set. -
Specify
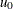 with the U0= option or with the variable
with the U0= option or with the variable _U_in a LIMITS= data set.
