Constructing Charts for Numbers of Nonconformities (c Charts)

Previous Page|Next Page

Constructing Charts for Numbers of Nonconformities (c Charts)

The following notation is used in this section:

expected number of nonconformities per unit produced by the process

$u_{i}$

number of nonconformities per unit in the ith subgroup

$c_{i}$

total number of nonconformities in the ith subgroup

$n_{i}$

number of inspection units in the ith subgroup. Typically, $n_{i} = 1$ and for c charts. In general, $u_{i}=c_{i}/n_{i}$ .

$\bar{u}$

average number of nonconformities per unit taken across subgroups. The quantity $\bar{u}$ is computed as a weighted average:

$\bar{u} = \frac{n_{1}u_{1} + \cdots + n_{N}u_{N}}{n_{1} + \cdots + n_{N}} = \frac{c_{1} + \cdots + c_{N}}{n_{1} + \cdots + n_{N}}$

number of subgroups

$\chi ^{2}_{\nu }$

has a central $\chi ^{2}$ distribution with $\nu$ degrees of freedom

Plotted Points

Each point on a c chart represents the total number of nonconformities ( $c_{i}$ ) in a subgroup. For example, Figure 17.24 displays three sections of pipeline that are inspected for defective welds (indicated by an X). Each section represents a subgroup composed of a number of inspection units, which are 1000-foot-long sections. The number of units in the ith subgroup is denoted by $n_{i}$ , which is the subgroup sample size. The value of $n_{i}$ can be fractional; Figure 17.24 shows $n_{3}=2.5$ units in the third subgroup.

Figure 17.24: Terminology for c Charts and u Charts

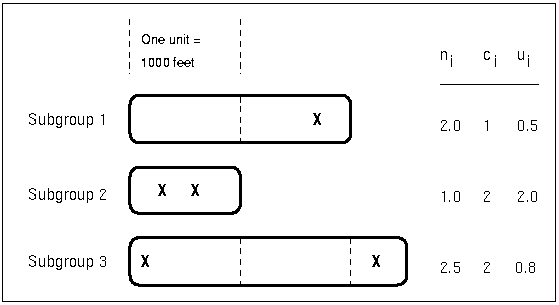
The number of nonconformities in the ith subgroup is denoted by $c_{i}$ . The number of nonconformities per unit in the ith subgroup is denoted by $u_{i}=c_{i}/n_{i}$ . In Figure 17.24, the number of welds per inspection unit in the third subgroup is $u_{3}=2/2.5=0.8$ .

A u chart created with the UCHART statement plots the quantity $u_{i}$ for the ith subgroup (see UCHART Statement: SHEWHART Procedure). An advantage of a u chart is that the value of the central line at the ith subgroup does not depend on $n_{i}$ . This is not the case for a c chart, and consequently, a u chart is often preferred when the number of units $n_{i}$ is not constant across subgroups.

Central Line

On a c chart, the central line indicates an estimate for $n_{i}u$ , which is computed as $n_{i}\bar{u}$ . If you specify a known value ( $u_{0}$ ) for u, the central line indicates the value of $n_{i}u_{0}$ .

Note that the central line varies with subgroup sample size $n_{i}$ . When $n_{i}=1$ for all subgroups, the central line has the constant value $\bar{c} = (c_{1} + \cdots + c_{N})/N$ .

Control Limits

You can compute the limits in the following ways:

as a specified multiple (k) of the standard error of 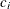$c_{i}$ above and below the central line. The default limits are computed with k = 3 (these are referred to as 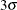$3\sigma$ limits).
as probability limits defined in terms of $\alpha$ , a specified probability that 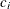$c_{i}$ exceeds the limits

The lower and upper control limits, LCLC and UCLC respectively, are given by

$\displaystyle \mbox{LCLC}$	$\displaystyle =$	$\displaystyle \mbox{max}\left(n_{i}\bar{u} - k\sqrt {n_{i}\bar{u}}\; ,0 \right)$
$\displaystyle \mbox{UCLC}$	$\displaystyle =$	$\displaystyle n_{i}\bar{u}+ k\sqrt {n_{i}\bar{u}}$

The upper and lower control limits vary with the number of inspection units per subgroup $n_{i}$ . If for all subgroups, the control limits have constant values.

$\displaystyle \mbox{LCLC}$	$\displaystyle =$	$\displaystyle \mbox{max}\left(\bar{c} - k\sqrt {\bar{c}}\; ,0 \right)$
$\displaystyle \mbox{UCLC}$	$\displaystyle =$	$\displaystyle \bar{c}+ k\sqrt {\bar{c}}$

An upper probability limit UCLC for $c_{i}$ can be determined using the fact that

$\begin{array}{ll} P\{ c_{i} > \mbox{UCLC}\} & = 1 - P\{ c_{i} \leq \mbox{UCLC} \} \\ & = 1 - P\{ \chi ^{2}_{2(\! {\mbox{\scriptsize UCLC}}+1)} \geq 2n_{i}\bar{u}\} \end{array}$

The upper probability limit UCLC is then calculated by setting

$1 - P\{ \chi ^{2}_{2(\! {\mbox{\scriptsize UCLC}}+1)} \geq 2n_{i}\bar{u}\} = \alpha /2$

and solving for UCLC.

A similar approach is used to calculate the lower probability limit LCLC, using the fact that

$P\{ c_{i} < \mbox{LCLC}\} = P\{ \chi ^{2}_{2(\! {\mbox{\scriptsize LCLC}}+1)} > 2n_{i}\bar{u}\}$

The lower probability limit LCLC is then calculated by setting

$P\{ \chi ^{2}_{2(\! {\mbox{\scriptsize LCLC}}+1)} > 2n_{i}\bar{u}\} = \alpha /2$

and solving for LCLC. This assumes that the process is in statistical control and that $c_{i}$ has a Poisson distribution. For more information, refer to Johnson, Kotz, and Kemp (1992). Note that the probability limits vary with the number of inspection units per subgroup () and are asymmetric about the central line.

If a standard value $u_{0}$ is available for u, replace $\bar{u}$ with in the formulas for the control limits. You can specify parameters for the limits as follows:

Specify k with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set.
Specify $\alpha$ with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.
Specify a constant nominal sample size 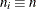$n_{i} \equiv n$ for the control limits with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.
Specify 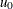$u_{0}$ with the U0= option or with the variable _U_ in a LIMITS= data set.

CCHART Statement: SHEWHART Procedure

Constructing Charts for Numbers of Nonconformities (c Charts)

Plotted Points

Central Line

Control Limits