PROC CAPABILITY and General Statements
Standard Capability Indices
This section provides computational details for the standard process capability indices computed by the CAPABILITY procedure:
![]() , CPL, CPU,
, CPL, CPU, ![]() , and
, and ![]() .
.
The Index Cp
The process capability index ![]() , sometimes called the “process potential index,” the “process capability ratio,” or the “inherent capability index,” is estimated as
, sometimes called the “process potential index,” the “process capability ratio,” or the “inherent capability index,” is estimated as
|
|
where USL is the upper specification limit, LSL is the lower specification limit, and s is the sample standard deviation. If you do not specify both the upper and the lower specification limits in the SPEC statement
or the SPEC= data set, then ![]() is assigned a missing value.
is assigned a missing value.
The interpretation of ![]() can depend on the application, on past experience, and on local practice. However, broad guidelines for interpretation have
been proposed by several authors. Ekvall and Juran (1974) classify
can depend on the application, on past experience, and on local practice. However, broad guidelines for interpretation have
been proposed by several authors. Ekvall and Juran (1974) classify ![]() values as
values as
-
“not adequate” if
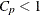
-
“adequate” if
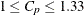 , but requiring close control as
, but requiring close control as 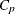 approaches 1
approaches 1
-
“more than adequate” if
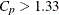
Montgomery (1996) recommends minimum values of ![]() as
as
-
1.33 for existing processes
-
1.50 for new processes or for existing processes when the variable is critical (for example, related to safety or strength)
-
1.67 for new processes when the variable is critical
Exact ![]() lower and upper confidence limits for
lower and upper confidence limits for ![]() (denoted by LCL and UCL) are computed using percentiles of the chi-square distribution, as indicated by the following equations:
(denoted by LCL and UCL) are computed using percentiles of the chi-square distribution, as indicated by the following equations:
|
|
|
|
|
|
|
|
Here, ![]() denotes the lower
denotes the lower ![]() th percentile of the chi-square distribution with
th percentile of the chi-square distribution with ![]() degrees of freedom. Refer to Chou, Owen, and Borrego (1990) and Kushler and Hurley (1992).
degrees of freedom. Refer to Chou, Owen, and Borrego (1990) and Kushler and Hurley (1992).
You can specify ![]() with the ALPHA= option in the PROC CAPABILITY statement or with the CIINDICES( ALPHA=value ) in the PROC CAPABILITY statement. The default value is 0.05. You can save these limits in the OUT= data set by specifying
the keywords CPLCL and CPUCL in the OUTPUT statement. In addition, you can display these limits on plots produced by the CAPABILITY
procedure by specifying the keywords in the INSET statement.
with the ALPHA= option in the PROC CAPABILITY statement or with the CIINDICES( ALPHA=value ) in the PROC CAPABILITY statement. The default value is 0.05. You can save these limits in the OUT= data set by specifying
the keywords CPLCL and CPUCL in the OUTPUT statement. In addition, you can display these limits on plots produced by the CAPABILITY
procedure by specifying the keywords in the INSET statement.
The Index CPL
The process capability index CPL is estimated as
|
|
where ![]() is the sample mean, LSL is the lower specification limit, and s is the sample standard deviation. If you do not specify the lower specification limit in the SPEC statement or the SPEC=
data set, then CPL is assigned a missing value.
is the sample mean, LSL is the lower specification limit, and s is the sample standard deviation. If you do not specify the lower specification limit in the SPEC statement or the SPEC=
data set, then CPL is assigned a missing value.
Montgomery (1996) refers to CPL as the “process capability ratio” in the case of one-sided lower specifications and recommends minimum values as follows:
-
1.25 for existing processes
-
1.45 for new processes or for existing processes when the variable is critical
-
1.60 for new processes when the variable is critical
Exact ![]() lower and upper confidence limits for CPL are computed using a generalization of the method of Chou, Owen, and Borrego (1990), who point out that the
lower and upper confidence limits for CPL are computed using a generalization of the method of Chou, Owen, and Borrego (1990), who point out that the ![]() lower confidence limit for CPL (denoted by CPLLCL )satisfies the equation
lower confidence limit for CPL (denoted by CPLLCL )satisfies the equation
|
|
where ![]() has a non-central t distribution with n – 1 degrees of freedom and noncentrality parameter
has a non-central t distribution with n – 1 degrees of freedom and noncentrality parameter ![]() . You can specify
. You can specify ![]() with the ALPHA= option in the PROC CAPABILITY statement. The default value is 0.05. The confidence limits can be saved in
an output data set by specifying the keywords CPLLCL and CPLUCL in the OUTPUT statement. In addition, you can display these
limits on plots produced by the CAPABILITY procedure by specifying these keywords in the INSET statement.
with the ALPHA= option in the PROC CAPABILITY statement. The default value is 0.05. The confidence limits can be saved in
an output data set by specifying the keywords CPLLCL and CPLUCL in the OUTPUT statement. In addition, you can display these
limits on plots produced by the CAPABILITY procedure by specifying these keywords in the INSET statement.
The Index CPU
The process capability index CPU is estimated as
|
|
where USL is the upper specification limit, ![]() is the sample mean, and s is the sample standard deviation. If you do not specify the upper specification limit in the SPEC statement or the SPEC=
data set, then CPU is assigned a missing value.
is the sample mean, and s is the sample standard deviation. If you do not specify the upper specification limit in the SPEC statement or the SPEC=
data set, then CPU is assigned a missing value.
Montgomery (1996) refers to CPU as the “process capability ratio” in the case of one-sided upper specifications and recommends minimum values that are the same as those specified previously for CPL.
Exact ![]() lower and upper confidence limits for CPU are computed using a generalization of the method of Chou, Owen, and Borrego (1990), who point out that the
lower and upper confidence limits for CPU are computed using a generalization of the method of Chou, Owen, and Borrego (1990), who point out that the ![]() lower confidence limit for CPU (denoted by CPULCL )satisfies the equation
lower confidence limit for CPU (denoted by CPULCL )satisfies the equation
|
|
where ![]() has a non-central t distribution with n – 1 degrees of freedom and noncentrality parameter
has a non-central t distribution with n – 1 degrees of freedom and noncentrality parameter ![]() . You can specify
. You can specify ![]() with the ALPHA= option in the PROC CAPABILITY statement. The default value is 0.05. The confidence limits can be saved in
an output data set by specifying the keywords CPULCL and CPUUCL in the OUTPUT statement. In addition, you can display these
limits on plots produced by the CAPABILITY procedure by specifying these keywords in the INSET statement.
with the ALPHA= option in the PROC CAPABILITY statement. The default value is 0.05. The confidence limits can be saved in
an output data set by specifying the keywords CPULCL and CPUUCL in the OUTPUT statement. In addition, you can display these
limits on plots produced by the CAPABILITY procedure by specifying these keywords in the INSET statement.
The Index Cpk
The process capability index ![]() is defined as
is defined as
|
|
Note that the indices ![]() ,
, ![]() , and k are related as
, and k are related as ![]() . The CAPABILITY procedure estimates
. The CAPABILITY procedure estimates ![]() as
as
|
|
where USL is the upper specification limit, LSL is the lower specification limit, ![]() is the sample mean, and s is the sample standard deviation.
is the sample mean, and s is the sample standard deviation.
If you specify only the upper limit in the SPEC statement or the SPEC= data set, then ![]() is computed as CPU, and if you specify only the lower limit in the SPEC statement or the SPEC= data set, then
is computed as CPU, and if you specify only the lower limit in the SPEC statement or the SPEC= data set, then ![]() is computed as CPL.
is computed as CPL.
Bissell (1990) derived approximate two-sided 95% confidence limits for ![]() by assuming that the distribution of
by assuming that the distribution of ![]() is normal. Using Bissell’s approach, 100
is normal. Using Bissell’s approach, 100![]() % lower and upper confidence limits can be computed as
% lower and upper confidence limits can be computed as
|
|
|
![$\displaystyle \widehat{C}_{pk} \left[ 1 - \Phi ^{-1}(1-\alpha /2 ) \sqrt { \frac{1}{9n \widehat{C}_{pk}^{2} } + \frac{1}{2(n-1)} } \; \right] $](images/qcug_capability0226.png) |
|
|
|
![$\displaystyle \widehat{C}_{pk} \left[ 1 + \Phi ^{-1}( 1-\alpha /2 ) \sqrt { \frac{1}{9n \widehat{C}_{pk}^{2} } + \frac{1}{2(n-1)} } \; \right] $](images/qcug_capability0227.png) |
where ![]() denotes the cumulative standard normal distribution function. Kushler and Hurley (1992) concluded that Bissell’s method gives reasonably accurate results.
denotes the cumulative standard normal distribution function. Kushler and Hurley (1992) concluded that Bissell’s method gives reasonably accurate results.
You can specify ![]() with the ALPHA= option in the PROC CAPABILITY statement. The default value is 0.05. These limits can be saved in an output
data set by specifying the keywords CPKLCL and CPKUCL in the OUTPUT statement. In addition, you can display these limits on
plots produced by the CAPABILITY procedure by specifying these same keywords in the INSET statement.
with the ALPHA= option in the PROC CAPABILITY statement. The default value is 0.05. These limits can be saved in an output
data set by specifying the keywords CPKLCL and CPKUCL in the OUTPUT statement. In addition, you can display these limits on
plots produced by the CAPABILITY procedure by specifying these same keywords in the INSET statement.
The Index Cpm
The process capability index ![]() is intended to account for deviation from the target T in addition to variability from the mean. This index is often defined as
is intended to account for deviation from the target T in addition to variability from the mean. This index is often defined as
|
|
A closely related version of ![]() is the index
is the index
|
|
where ![]() and
and ![]() . If
. If ![]() , then
, then ![]() . However, if
. However, if ![]() , then both indices suffer from problems of interpretation, as pointed out by Kotz and Johnson (1993), and their use should be avoided in this case.
, then both indices suffer from problems of interpretation, as pointed out by Kotz and Johnson (1993), and their use should be avoided in this case.
The CAPABILITY procedure computes an estimator of ![]() as
as
|
|
where s is the sample standard deviation.
If you specify only a single specification limit SL in the SPEC statement or the SPEC= data set, then ![]() is estimated as
is estimated as
|
|
Boyles (1991) proposed a slightly modified point estimate for ![]() computed as
computed as
|
|
Boyles also suggested approximate two-sided 100![]() % confidence limits for
% confidence limits for ![]() , which are computed as
, which are computed as
|
|
|
|
|
|
|
|
Here ![]() denotes the lower
denotes the lower ![]() th percentile of the chi-square distribution with
th percentile of the chi-square distribution with ![]() degrees of freedom, where
degrees of freedom, where ![]() equals
equals
|
|
You can specify ![]() with the ALPHA= option in the PROC CAPABILITY statement. The default value is 0.05. These confidence limits can be saved
in an output data set by specifying the keywords CPMLCL and CPMUCL in the OUTPUT statement. In addition, you can display these
limits on plots produced by the CAPABILITY procedure by specifying these keywords in the INSET statement.
with the ALPHA= option in the PROC CAPABILITY statement. The default value is 0.05. These confidence limits can be saved
in an output data set by specifying the keywords CPMLCL and CPMUCL in the OUTPUT statement. In addition, you can display these
limits on plots produced by the CAPABILITY procedure by specifying these keywords in the INSET statement.
