PCHART Statement: ANOM Procedure
Constructing ANOM Charts for Proportions
The following notation is used in this section:
|
|
response number (count) in the ith group |
|
|
k |
number of groups |
|
|
|
sample size of the ith group |
|
|
N |
total sample size |
|
|
|
proportion in the ith group, where |
|
|
|
weighted average of proportions across groups:
|
|
|
|
significance level |
|
|
|
critical value for ANOM for normal data in the balanced case |
|
|
|
critical value for ANOM for normal data in the unbalanced case |
Central Line
By default, the central line on an ANOM p chart is computed as ![]() , the weighted average of the group proportions. You can specify
, the weighted average of the group proportions. You can specify ![]() with the P= option or with the variable
with the P= option or with the variable _P_ in a LIMITS= data set.
Decision Limits
For the ith group, the response counts are assumed to have the binomial distribution ![]() . The ANOM method for proportions tests the null hypothesis that
. The ANOM method for proportions tests the null hypothesis that ![]() , that is, that the proportions are the same, against the alternative that at least one of the
, that is, that the proportions are the same, against the alternative that at least one of the ![]() ’s is different from the average of the k proportions.
’s is different from the average of the k proportions.
The decision limits are computed using the normal approximation to the binomial distribution, which is appropriate when the
sample sizes for the groups are large; refer to Ramig (1983). A commonly recommended check for this assumption is that ![]() and
and ![]() for all the groups. The critical values in the ANOM method for normally distributed data are adapted to the binomial case
by using infinite degrees of freedom for the variance.
for all the groups. The critical values in the ANOM method for normally distributed data are adapted to the binomial case
by using infinite degrees of freedom for the variance.
When the sample sizes are constant across groups (![]() ), the decision limits are computed as follows:
), the decision limits are computed as follows:
|
|
|
|
|
|
|
|
For the theoretical derivation of the decision limits, refer to Nelson (1982a).
When the sample sizes (![]() ) are different across groups (the unbalanced case), the decision limits are computed as follows:
) are different across groups (the unbalanced case), the decision limits are computed as follows:
|
|
|
|
|
|
|
|
Note that the decision limits for the ith group depend on ![]() . If the sample sizes are constant across groups (
. If the sample sizes are constant across groups (![]() ), the decision limits in the unbalanced case reduce to the formulas given for the balanced case since
), the decision limits in the unbalanced case reduce to the formulas given for the balanced case since ![]() and
and ![]() so
so
|
|
For the derivation of the decision limits for unequal sample sizes, refer to Nelson (1991).
Exact critical values ![]() were first tabulated by L. S. Nelson (1983). Refer to Nelson (1993) for derivation of critical values.
were first tabulated by L. S. Nelson (1983). Refer to Nelson (1993) for derivation of critical values.
You can specify parameters for the limits as follows:
-
Specify
 with the ALPHA= option or with the variable
with the ALPHA= option or with the variable _ALPHA_in a LIMITS= data set. By default, =
= 0.05. -
Specify a constant nominal sample size
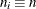 for the decision limits with the LIMITN= option or with the variable
for the decision limits with the LIMITN= option or with the variable _LIMITN_in a LIMITS= data set. By default, n is the observed sample size in the balanced case. -
Specify
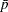 with the P= option or with the variable
with the P= option or with the variable _P_in a LIMITS= data set. By default,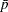 is the weighted average of the group proportions.
is the weighted average of the group proportions.
