| Nonnormal Process Data |
[See SHWNONN in the SAS/QC Sample Library]A number of authors have pointed out that Shewhart charts for subgroup means work well whether the measurements are normally distributed or not.1 On the other hand, the interpretation of standard control charts for individual measurements (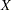 charts) is affected by departures from normality.
charts) is affected by departures from normality.
In situations involving a large number of measurements, it may be possible to subgroup the data and construct an 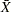 chart instead of an
chart instead of an 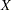 chart. However, the measurements should not be subgrouped arbitrarily for this purpose.2 If subgrouping is not possible, two alternatives are to transform the data to normality (preferably with a simple transformation such as the log transformation) or modify the usual limits based on a suitable model for the data distribution.
chart. However, the measurements should not be subgrouped arbitrarily for this purpose.2 If subgrouping is not possible, two alternatives are to transform the data to normality (preferably with a simple transformation such as the log transformation) or modify the usual limits based on a suitable model for the data distribution.
The second of these alternatives is illustrated here with data from a study conducted by a service center. The time taken by staff members to answer the phone was measured, and the delays were saved as values of a variable named Time in a SAS data set named Calls. A partial listing of Calls is shown in Figure 15.216.
| Recnum | Time |
|---|---|
| 1 | 3.233 |
| 2 | 3.110 |
| 3 | 3.136 |
| 4 | 2.899 |
| 5 | 2.838 |
| 6 | 2.459 |
| 7 | 3.716 |
| 8 | 2.740 |
| 9 | 2.487 |
| 10 | 2.635 |
| 11 | 2.676 |
| 12 | 2.905 |
| 13 | 3.431 |
| 14 | 2.663 |
| 15 | 3.437 |
| 16 | 2.823 |
| 17 | 2.596 |
| 18 | 2.633 |
| 19 | 3.235 |
| 20 | 2.701 |
| 21 | 3.202 |
| 22 | 2.725 |
| 23 | 3.151 |
| 24 | 2.464 |
| 25 | 2.662 |
| 26 | 3.188 |
| 27 | 2.640 |
| 28 | 2.541 |
| 29 | 3.033 |
| 30 | 2.993 |
| 31 | 2.636 |
| 32 | 2.481 |
| 33 | 3.191 |
| 34 | 2.662 |
| 35 | 2.967 |
| 36 | 3.300 |
| 37 | 2.530 |
| 38 | 2.777 |
| 39 | 3.353 |
| 40 | 3.614 |
| 41 | 4.288 |
| 42 | 2.442 |
| 43 | 2.552 |
| 44 | 2.613 |
| 45 | 2.731 |
| 46 | 2.780 |
| 47 | 3.588 |
| 48 | 2.612 |
| 49 | 2.579 |
| 50 | 2.871 |
Footnotes
- Refer to Schilling and Nelson (1976) and Wheeler (1991).
- Refer to Wheeler and Chambers (1986) for a discussion of subgrouping.