PROC RELIABILITY: Parametric Model for Interval Recurrent Events Data

Parametric Model for Interval Recurrent Events Data

Byar (1980) provides data for recurrences of bladder tumors in patients in a clinical trial. Figure 14.49 is a partial listing of data for 86 patients, of which 48 were given a placebo and 38 were treated with the drug Thiotepa. The data are here grouped into one month intervals.

Figure 14.49 Partial Listing of the Bladder Tumor Data

Obs	Group	Age	Age1	N	R
1	Placebo	0	1	48	0
2	Placebo	1	2	47	0
3	Placebo	2	3	46	1
4	Placebo	3	4	46	4
5	Placebo	4	5	46	7
6	Placebo	5	6	45	0
7	Placebo	6	7	45	2
8	Placebo	7	8	45	4
9	Placebo	8	9	44	1
10	Placebo	9	10	44	2
11	Placebo	10	11	44	4
12	Placebo	11	12	42	2
13	Placebo	12	13	42	1
14	Placebo	13	14	42	4
15	Placebo	14	15	42	1
16	Placebo	15	16	41	1
17	Placebo	16	17	41	5
18	Placebo	17	18	41	4
19	Placebo	18	19	41	4
20	Placebo	19	20	38	1

The following SAS statements fit a nonhomogeneous Poisson process model with a power intensity function to the interval recurrence data. Some patients were lost to follow-up in each month, so the number of patients observed changes from month to month. The variable N provides the number of patients available at the beginning of each month and assumed to be observed throughout the month. The variable R is the number of recurrences of tumors in each month. Age represents the number of months after randomization into the trial (starting with month 0), and Age1=Age+1 is the end of a month. The variable Group represents the treatment, either Placebo or Thiotepa. The MODEL statement requests a maximum likelihood fit of the model with Group as a classification variable. The MCFPLOT statement requests a plot of the fitted model and nonparametric estimates of the mean cumulative function for each group.

proc reliability data=Tumor;
   distribution nhpp(pow);
   freq R;
   nenter N;
   class Group;
   model  (Age Age1) = Group;
   mcfplot(Age Age1) = Group / fit=model noconf;
run;

The resulting maximum likelihood parameter estimates are shown in Figure 14.50.

Figure 14.50 Power Model Parameter Estimates for the Bladder Tumor Data

The RELIABILITY Procedure

NHPP-Power Parameter Estimates
Parameter		Estimate	Standard Error	Asymptotic Normal
				95% Confidence Limits
				Lower	Upper
Intercept		23.5802	3.1567	17.3932	29.7671
Group	Placebo	-4.3826	3.4873	-11.2175	2.4523
Group	Thiotepa	0.0000	0.0000	0.0000	0.0000
Shape		1.1682	0.0960	0.9945	1.3723

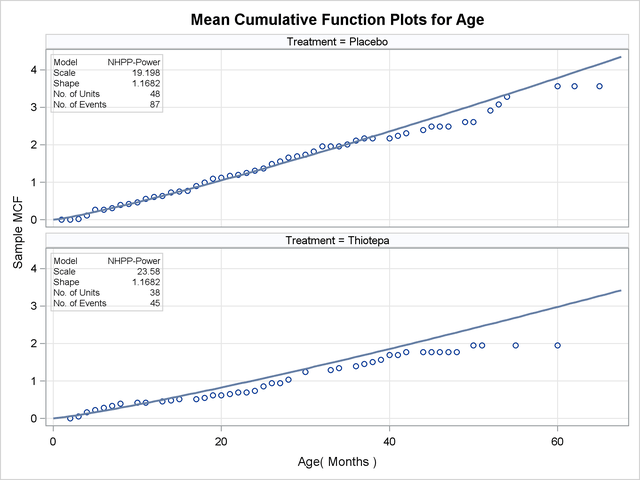
Nonparametric estimates of the mean cumulative function are plotted as points, and the fitted model is plotted as the solid line in Figure 14.51.

Figure 14.51 Mean Cumulative Function Plot for the Bladder Tumor Data