Example 12.5 Optimal Design Using a Small Candidate Set
[See OPTEX4 in the SAS/QC Sample Library]This example is a continuation of Example 12.4.
A well-chosen initial design can speed up the search procedure, as illustrated in Example 12.2. Another way to speed up the search is to reduce the candidate set. The following statements generate the optimal design with a fast, sequential search and then use the FREQ procedure to examine the frequency of different factor levels in the final design:
proc optex data=a seed=33805 noprint; model AFR|EGR|SA@2 AFR*AFR EGR*EGR SA*SA; generate n=50 method=sequential; output out=b; proc freq; table AFR EGR SA / nocum; run;
| AFR | Frequency | Percent |
|---|---|---|
| 15 | 19 | 38.00 |
| 16 | 6 | 12.00 |
| 17 | 6 | 12.00 |
| 18 | 19 | 38.00 |
| EGR | Frequency | Percent |
|---|---|---|
| 0.02 | 20 | 40.00 |
| 0.566 | 9 | 18.00 |
| 1.117 | 21 | 42.00 |
| SA | Frequency | Percent |
|---|---|---|
| 10 | 20 | 40.00 |
| 28 | 5 | 10.00 |
| 34 | 6 | 12.00 |
| 52 | 19 | 38.00 |
From Output 12.5.1, it is evident that most of the factor values lie in the middle or at the extremes of their respective ranges. This suggests looking for an optimal design with a candidate set that includes only those points in which the factors have values in the middle or at the extremes of their respective ranges. The following statements illustrate this approach (see Output 12.5.2):
proc plan;
factors AFR=4 ordered EGR=4 ordered SA=4 ordered
/ noprint;
output out=a AFR nvals=(15, 16, 17, 18)
EGR nvals=(0.020, 0.377, 0.566, 1.117)
SA nvals=(10, 28, 34, 52);
proc optex seed=61552;
model AFR|EGR|SA@2 AFR*AFR EGR*EGR SA*SA;
generate n=50 method=detmax;
run;
| Design Number | D-Efficiency | A-Efficiency | G-Efficiency | Average Prediction Standard Error |
|---|---|---|---|---|
| 1 | 46.5151 | 24.9003 | 96.7226 | 0.4442 |
| 2 | 46.4997 | 24.5549 | 96.1157 | 0.4478 |
| 3 | 46.4920 | 24.5530 | 95.9941 | 0.4480 |
| 4 | 46.4657 | 24.8653 | 95.5627 | 0.4446 |
| 5 | 46.4547 | 24.5071 | 96.0385 | 0.4481 |
| 6 | 46.4333 | 25.0321 | 95.1371 | 0.4448 |
| 7 | 46.4333 | 25.0321 | 95.1371 | 0.4448 |
| 8 | 46.4333 | 25.0321 | 95.1371 | 0.4448 |
| 9 | 46.3916 | 24.3617 | 95.0041 | 0.4489 |
| 10 | 46.3379 | 24.8695 | 94.3115 | 0.4458 |
The resulting design is about as good as the best one obtained from a complete candidate set (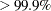 relative D-efficiency and marginally higher relative A-efficiency) and takes much less time to find.
relative D-efficiency and marginally higher relative A-efficiency) and takes much less time to find.
See the section Handling Many Variables for another example of reducing the candidate set for the optimal design search.