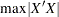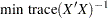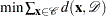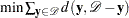Introduction to the OPTEX Procedure

Features

This section summarizes key features of the OPTEX procedure.

The OPTEX procedure offers various criteria for searching a design; these criteria are summarized in Table 12.1 and Table 12.2. In the formulas for these criteria, 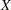$\text{[math]}$ denotes the design matrix, 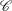$\text{[math]}$ the set of candidate points, and 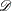$\text{[math]}$ the set of design points. The default criterion is D-optimality. You can also use the OPTEX procedure to generate G- and I-efficient designs.

The OPTEX procedure also offers a variety of search algorithms, ranging from a simple sequential search (Dykstra 1971) to the computer-intensive Fedorov algorithm (Fedorov 1972, Cook and Nachtsheim 1980). You can customize many aspects of the search, such as the initialization method and the number of iterations.

You can use the full general linear modeling facilities of the GLM procedure to specify a model for your design, allowing for general polynomial effects as well as classification or ANOVA effects. Optionally, you can specify

design points to be optimally augmented
fixed covariates (for example, blocks) for the design
prior precisions for Bayesian optimal design

The OPTEX procedure is an interactive procedure. After specifying an initial design, you can submit additional statements without reinvoking the OPTEX procedure. Once you have found a design, you can

examine the design
output the design to a data set
change the model and find another design
change the characteristics of the search and find another design

Table 12.1 Information-Based Optimality Criteria
Criterion	Goal	Formula
D-optimality	Maximize determinant of the	$\text{[math]}$
	information matrix
A-optimality	Minimize sum of the variances	$\text{[math]}$
	of estimated coefficients

Table 12.2 Distance-Based Optimality Criteria
Criterion	Goal	Formula
U-optimality	Minimize distance from	$\text{[math]}$
	design to candidates
S-optimality	Maximize distance	$\text{[math]}$
	between design points