Example 5.18 Approximate Confidence Limits for Cpk
[See CPKCON3 in the SAS/QC Sample Library]This example illustrates how you can use the OUTPUT statement to compute confidence limits for the capability index 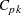 .
.
You can request the approximate confidence limits given by Bissell (1990) with the keywords CPKLCL and CPKUCL in the OUTPUT statement. However, this is not the only method that has been proposed for computing confidence limits for 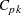 . Zhang, Stenback, and Wardrop (1990), referred to here as ZSW, proposed approximate confidence limits of the form
. Zhang, Stenback, and Wardrop (1990), referred to here as ZSW, proposed approximate confidence limits of the form
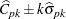 |
where 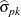 is an estimator of the standard deviation of
is an estimator of the standard deviation of 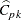 . Equation (8) of ZSW provides an approximation to the variance of
. Equation (8) of ZSW provides an approximation to the variance of 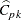 from which one can obtain 100
from which one can obtain 100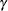 % confidence limits for
% confidence limits for 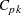 as
as
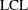 |
 |
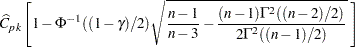 |
|||
 |
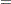 |
 |
This assumes that  is normally distributed. You can also compute approximate confidence limits based on equation (6) of ZSW, which provides an exact expression for the variance of
is normally distributed. You can also compute approximate confidence limits based on equation (6) of ZSW, which provides an exact expression for the variance of  .
.
The following program uses the methods of Bissell (1990) and ZSW to compute approximate confidence limits for 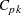 for the variable Hardness in the data set Titanium (see Example 5.17).
for the variable Hardness in the data set Titanium (see Example 5.17).
proc capability data=Titanium noprint;
var Hardness;
specs lsl=0.8 usl=2.4;
output out=Summary
n = n
mean = mean
std = std
lsl = lsl
usl = usl
cpk = cpk
cpklcl = cpklcl
cpkucl = cpkucl
cpl = cpl
cpu = cpu ;
data Summary;
set Summary;
length Method $ 16;
Method = "Bissell";
lcl = cpklcl;
ucl = cpkucl;
output;
* Assign confidence level;
level = 0.95;
aux = probit( 1 - (1-level)/2 );
Method = "ZSW Equation 6";
zsw = log(0.5*n-0.5)
+ ( 2*(lgamma(0.5*n-1)-lgamma(0.5*n-0.5)) );
zsw = sqrt((n-1)/(n-3)-exp(zsw));
lcl = cpk*(1-aux*zsw);
ucl = cpk*(1+aux*zsw);
output;
Method = "ZSW Equation 8";
ds = 3*(cpu+cpl)/2;
ms = 3*(cpl-cpu)/2;
f1 = (1/3)*sqrt((n-1)/2)*gamma((n-2)/2)*(1/gamma((n-1)/2));
f2 = sqrt(2/n)*(1/gamma(0.5))*exp(-n*0.5*ms*ms);
f3 = ms*(1-(2*probnorm(-sqrt(n)*ms)));
ex = f1*(ds-f2-f3);
sd = ((n-1)/(9*(n-3)))*(ds**2-(2*ds*(f2+f3))+ms**2+(1/n));
sd = sd-(ex*ex);
sd = sqrt(sd);
lcl = cpk-aux*sd;
ucl = cpk+aux*sd;
output;
run;
title "Approximate 95% Confidence Limits for Cpk"; proc print data = Summary noobs; var Method lcl cpk ucl; run;
The results are shown in Output 5.18.1.
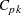
| Approximate 95% Confidence Limits for Cpk |
| Method | lcl | cpk | ucl |
|---|---|---|---|
| Bissell | 1.43845 | 1.80818 | 2.17790 |
| ZSW Equation 6 | 1.43596 | 1.80818 | 2.18040 |
| ZSW Equation 8 | 1.42419 | 1.80818 | 2.19217 |
Note that there is fairly close agreement in the three methods.
You can display the confidence limits computed using Bissell’s approach on plots produced by the CAPABILITY procedure by specifying the keywords CPKLCL and CPKUCL in the INSET statement.
The following statements also compute an estimate of the index 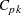 along with approximate limits by using the SPECIALINDICES option:
along with approximate limits by using the SPECIALINDICES option:
proc capability data=Titanium specialindices; var Hardness; specs lsl=0.8 usl=2.4; run;
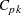 using the SPECIALINDICES option
using the SPECIALINDICES option
| Approximate 95% Confidence Limits for Cpk |
| Process Capability Indices | |||
|---|---|---|---|
| Index | Value | 95% Confidence Limits | |
| Cp | 2.005745 | 1.609575 | 2.401129 |
| CPL | 1.808179 | 1.438675 | 2.175864 |
| CPU | 2.203311 | 1.757916 | 2.646912 |
| Cpk | 1.808179 | 1.438454 | 2.177904 |
