UCHART Statement: ANOM Procedure
Creating ANOM Charts for Rates from Group Counts
[See ANMU1 in the SAS/QC Sample Library]A health care system administrator uses ANOM to compare medical/surgical admissions rates for set of clinics. For more background concerning this application, refer to Rodriguez (1996).
The following statements create a SAS data set named MSAdmits, which contains the number of admissions and the number of member-months for each clinic during a one-year period.
data MSAdmits; length ID $ 2; input ID Count MemberMonths @@; KMemberYrs = MemberMonths/12000; label ID = 'Medical Group Id Number'; datalines; 1A 1882 697204 1K 600 224715 1B 438 154720 1D 318 82254 3M 183 76450 3I 220 73529 1N 121 60169 3H 105 52886 1Q 124 52595 1E 171 51229 3B 88 34775 1C 100 31959 1H 112 28782 3C 84 27478 1R 69 26494 1T 21 25096 1M 130 24723 1O 61 24526 3D 66 22359 1J 54 19101 3J 30 16089 3G 36 13851 3E 26 10587 1G 28 10351 1I 25 6041 1L 20 5138 1S 7 2723 1F 7 2424 1P 2 2030 ; proc sort data=MSAdmits; by ID; run;
A partial listing of MSAdmits is shown in Figure 4.17.
| Medical/Surgical Admissions |
| ID | Count | MemberMonths | KMemberYrs |
|---|---|---|---|
| 1A | 1882 | 697204 | 58.1003 |
| 1B | 438 | 154720 | 12.8933 |
| 1C | 100 | 31959 | 2.6633 |
| 1D | 318 | 82254 | 6.8545 |
| 1E | 171 | 51229 | 4.2691 |
| 1F | 7 | 2424 | 0.2020 |
| 1G | 28 | 10351 | 0.8626 |
| 1H | 112 | 28782 | 2.3985 |
| 1I | 25 | 6041 | 0.5034 |
| 1J | 54 | 19101 | 1.5918 |
There is a single observation per clinic. The variable ID identifies the clinics and is referred to as the group-variable. The variable Count provides the number of admissions for each clinic, which is referred to as the response variable (or response for short). The variable MemberMonths, which provides the number of member-months for each clinic, is divided by 1200 to compute the variable KMemberYrs, the number of 1000-member-years, which serves as the measure of opportunity for an admission to occur.
The following example illustrates the basic form of the UCHART statement. After the keyword UCHART, you specify the response to analyze (in this case, Count), followed by an asterisk and the group-variable (ID).
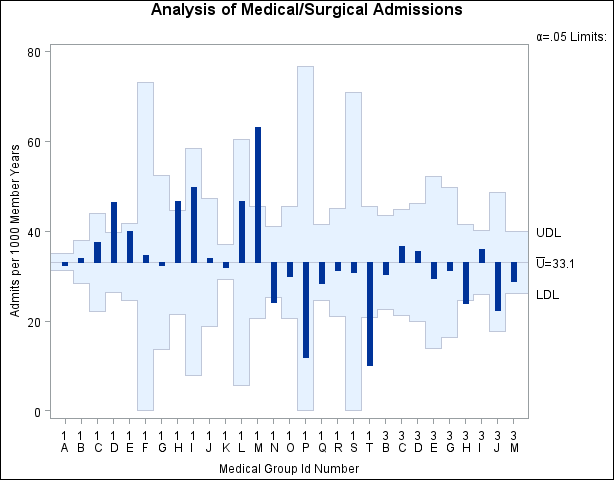
The following statements create the  chart shown in Figure 4.18:
chart shown in Figure 4.18:
ods graphics off;
title 'Analysis of Medical/Surgical Admissions';
proc anom data=MSAdmits;
uchart Count*ID / groupn = KMemberYrs
turnhlabels
nolegend;
label Count = 'Admits per 1000 Member Years';
run;
The TURNHLABELS option is used to vertically display the horizontal axis labels. The GROUPN= option specifies the number of "occurrence opportunity" units in each group and is required if the input data set is a DATA= data set. In this example, 1000 member years represent one unit of opportunity. The number of units per group can be thought of as the group "sample size." You can use the GROUPN= option to specify one of the following:
a constant number of units, which applies to all the groups
an input variable name, which provides the number of units for each group (KMemberYrs in this example)
Options such as GROUPN= are specified after the slash (/) in the UCHART statement. A complete list of options is presented in the section Syntax: UCHART Statement.
 Chart Example
Chart Example
The input data set is specified with the DATA= option in the PROC ANOM statement.
Each point on the  chart represents the rate of occurrence, computed as the count divided by the number of opportunity units. The points are displayed in the sort order for the group-variable ID. The chart shows that Clinics 1D, 1H, and 1M have significantly higher admissions rates, and Clinics 1N, 1T, and 3H have significantly lower admissions rates.
chart represents the rate of occurrence, computed as the count divided by the number of opportunity units. The points are displayed in the sort order for the group-variable ID. The chart shows that Clinics 1D, 1H, and 1M have significantly higher admissions rates, and Clinics 1N, 1T, and 3H have significantly lower admissions rates.
By default, the decision limits correspond to a significance level of 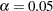 . This means that, assuming all clinics have the same rate of admissions, there is a 0.05 probability that one or more of the decision limits would be exceeded purely by chance. The formulas for the limits are given in the section Decision Limits. Note that the decision limits vary with the number of 1000-member-years for each clinic.
. This means that, assuming all clinics have the same rate of admissions, there is a 0.05 probability that one or more of the decision limits would be exceeded purely by chance. The formulas for the limits are given in the section Decision Limits. Note that the decision limits vary with the number of 1000-member-years for each clinic.
For more details on reading count data, see DATA= Data Set.
