| The SHEWHART Procedure |
Step 2: Modeling the Trend
The next step is to model the trend as a function of hour. The 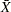 chart in Figure 13.43.48 suggests that the mean level of the process (saved as DiameterX in the OUTLIMITS= data set SUBMEANS) grows as the log of HOUR. The following statements fit a simple linear regression model in which DiameterX is the response variable and LOGHOUR (the log transformation of HOUR) is the predictor variable. Part of the printed output produced by PROC REG is shown in Figure 13.43.49.
chart in Figure 13.43.48 suggests that the mean level of the process (saved as DiameterX in the OUTLIMITS= data set SUBMEANS) grows as the log of HOUR. The following statements fit a simple linear regression model in which DiameterX is the response variable and LOGHOUR (the log transformation of HOUR) is the predictor variable. Part of the printed output produced by PROC REG is shown in Figure 13.43.49.
data submeans; set submeans; loghour=log(hour); run;
proc reg data=submeans ; model Diameterx=loghour; output out=regdata predicted=fitted ; run;
Output 13.43.49
Trend Analysis for Diameter from PROC REG
| Parameter Estimates | ||||||
|---|---|---|---|---|---|---|
| Variable | Label | DF | Parameter Estimate |
Standard Error |
t Value | Pr > |t| |
| Intercept | Intercept | 1 | 9.99056 | 0.02185 | 457.29 | <.0001 |
| loghour | 1 | 0.13690 | 0.00967 | 14.16 | <.0001 | |
Figure 13.43.49 shows that the fitted equation can be expressed as
 |
where  is the fitted subgroup average.1 A partial listing of the OUT= data set REGDATA created by the REG procedure is shown in Figure 13.43.50.
is the fitted subgroup average.1 A partial listing of the OUT= data set REGDATA created by the REG procedure is shown in Figure 13.43.50.
Output 13.43.50
Partial Listing of the Output Data Set regdata from the REG Procedure
Copyright © SAS Institute, Inc. All Rights Reserved.